16. Circular motion¶
16.1. Overview¶
Links to programs in this lesson:
Up to this point, we have only talked about situations with a constant acceleration. This gives rise to either motion along a line (such as a book sliding along a table) or at most, the parabolic motion we saw for projectiles. However, this does not exhaust all of the possibilities! We can consider cases where the direction of the acceleration changes, even if the magnitude does not. The prime example of this, and what we will look at in this lesson, is the case of uniform circular motion. This is motion that is “uniform” – the speed is constant (although the velocity will not be!) – and “circular” – the object in question moves in a circular path around a fixed point.
I am sure that you can think of many examples of uniform circular motion: a car driving around a circular track, a tetherball on its string as it circles the central pole, the Moon orbiting the Earth. In fact, the last case is an interesting historical story, since Newton used the Moon’s orbit to figure out that gravitation was a universal force acting on all objects. The distance to the Moon, and the time it takes to make one orbit, had been known since the time of the ancient Greeks. Newton used these numbers to calculate the magnitude of the Moon’s acceleration, and showed that it could be the result of a gravitational force between the Earth and the Moon if gravity acted in a particular way. We will explore this more when we get to gravitation in Lesson 21.
Here are the objectives for this lesson:
Define uniform circular motion.
State the magnitude and direction of the acceleration of an object in uniform circular motion.
Explain the relationship between centripetal force and net force on an object.
Solve for the speed of an object in uniform circular motion using Newton’s 2nd law.
Define central force
16.2. Circular motion¶
As defined above, uniform circular motion is the motion of an object at constant speed in a circular path around a point. Notice that velocity is not constant, since the instantaneous direction of the object’s motion at any point is changing; only the magnitude of the velocity is assumed to be the same.
Think about the examples of uniform circular motion listed in the first section above: a car driving around a circular track, a tetherball on its string as it circles the central pole, the Moon orbiting the Earth. Remember that Newton’s first law says that an object will continue with constant velocity unless acted on by a net force. Since all of these have changing velocity, their circular motion must be due to a net force (from Newton’s second law). What force or forces are causing this motion for each of the cases? It depends!
The force of friction keeps the car moving in a circle around the track. The easy way to see this is to think about what would happen on an icy track; which way would the car move then?
The gravitational force is responsible for the Moon’s circular orbit. In fact, as we will see in Lesson 25, it is actually that the Earth and the Moon are both orbiting around the center of mass of the Earth-Moon system! We don’t notice this effect, because the Earth has about 81 times the Moon’s mass.
For the tetherball on its tether, we have to be careful about what is causing the circular motion. It is definitely related to the tether, but not the entire force. If you draw an FBD for the system, the vertical part of the tension force is opposing the force of gravity, so the tetherball does not fall down. Only the horizontal component of the tension force is acting to keep the tetherball in a (horizontal) circle.

Fig. 16.1 Two children play during recess April 3, 2013, at Mountain Home Air Force Base, Idaho. Throughout the month the base is spotlighting these children and the struggles they go through as military kids. (source: U.S. Air Force photo by Airman 1st Class Malissa Lott/Released)¶
In each case, it was a different force (or component of a force) providing the net force necessary to change the velocity of the object, and keep it moving in a circle. This will be an important part of solving uniform circular motion problems – identifying what forces or forces create the motion.
Problem
A ping-pong ball is shot into a circular tube lying flat on a tabletop. When the ping-pong ball leaves the track, which path will it follow? Choose the letter of the best choice.
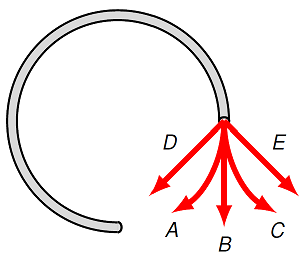
Fig. 16.2 Ping-pong ball moving through a tube¶
Answer: By Newton’s first law, an object will continue at a constant velocity whenever the net force on the object is zero. Once the ball leaves the tube, there is no more net force from the walls of the tube, so the ball moves in the straight line (path B).
Although the examples above are horizontal circles, circular motion applies to objects moving in a vertical wheel, such as a Ferris wheel or a jet in a vertical loop.
Problem
A bowling ball is rolled along a tile floor when a physicist comes along with a mallet. The physicist wants to hit the ball so that it moves in a circular path. Which way would the physicist have to hit the ball? (Answer the question first, then watch the video following this problem to check your choice!)
against the direction of motion
away from the center of the circle
in the direction of motion
towards the center of the circle
depends on the radius of the circle
16.3. Centripetal acceleration¶
If we imagine an object moving in a circle at constant speed, its acceleration is known as a centripetal acceleration, denoted by the symbol \({\vec a}_{cp}\). This comes from the Latin for “center-seeking”, and this is the direction of the centripetal acceleration: towards the center of the circle. Hopefully, you watched the video above of the bowling ball hit by a mallet, so the ball moves in a circle. When the ball is not hit, it moves in a straight line, as you would expect from Newton’s first law. When it is hit, the ball moves in a circle with its center in the direction of the mallet’s force. Later in this notebook, you will use a vPython simulation to see what happens when you choose different directions for the centripetal acceleration.
Before we get to that, however, let’s find what the magnitude of the centripetal acceleration is. Here is my favorite proof of this, which I originally found in a Khan Academy video (linked here). As the object moves in a circle, its velocity vector will always be of constant size (since the speed remains the same) and tangential to the circle (perpendicular to the radius). This looks like the picture shown below, with a ball moving in a clockwise circle.
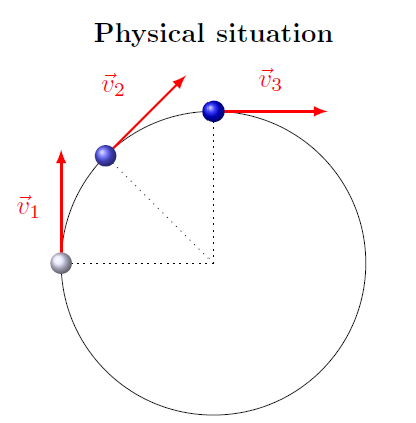
Fig. 16.4 Physical situation for a ball moving in a clockwise circle, with its position and velocity marked at three points¶
Since the ball is moving at a constant speed \(v\) around a circle with radius \(r\), then the time \(T\) to go once around the circle is related to the circumference by
The time \(T\) to complete one revolution around a circle is known as the period. Notice the velocity is always perpendicular to the radius vector from the center.
However, not only is the position of the ball rotating around in a circle, so is the velocity vector! The velocity is always tangential to the circle, so as the position angle changes, so does the direction of the velocity. So we can make a “velocity circle” by taking all of these velocities and placing their tails at the same point. Then the tips of all these vectors forms a circle as well. This is shown in the diagram below.
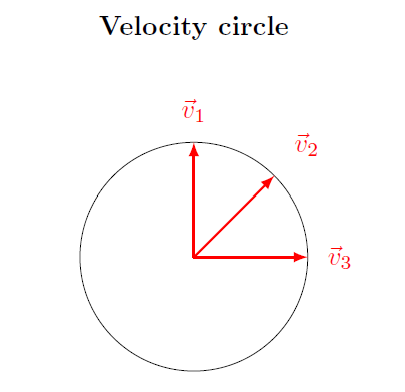
Fig. 16.5 Velocity circle, formed from the velocity vectors of the ball moving in the physical situation¶
The radius of this velocity circle is the magnitude \(v\) of the velocity; it takes the same period \(T\) for the velocity to rotate once around the circle. The rate of motion around the velocity circle is constant. If you think about it, this is just the acceleration!
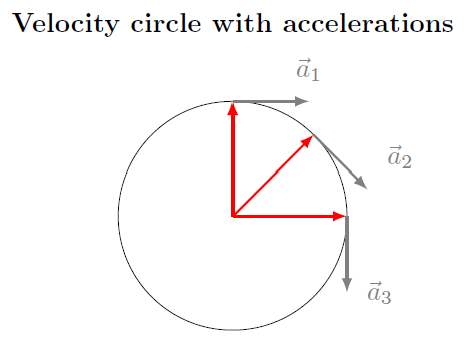
Fig. 16.6 Velocity circle, with acceleration vectors marked¶
For the physical situation, the position vector has a magnitude equal to the radius, and the velocity is tangential to the circle, while for the velocity circle, the velocity vector forms the radius of the circle, and the acceleration is tangential to the velocity circle.
If you think about how the velocity vector is changing in the velocity circle for small changes in time, this change \(\Delta {\vec v}\) must be tangential to the velocity, since the centripetal acceleration always points towards the circle’s center. Thus, the acceleration magnitude tells us how long it takes for the velocity to go once around the circle in one period, or
Now we can relate these two equations together, since the periods are the same. This means
This gives us the magnitude of the centripetal acceleration. To summarize,
Quantity: centripetal acceleration
Symbol: \({\vec a}_{cp}\)
Equation: The magnitude is given by
where \(v\) is the speed of an object moving in a circle, and \(r\) is the radius of that circle
Direction: “center-seeking” (centripetal)
Units: m/s\(^2\)
16.4. Circular motion in vPython¶
One of the most frequent mistakes I see students make with uniform circular motion is getting the direction of the centripetal acceleration wrong. Thus, I am putting some code here to see what goes wrong with the common guesses for this direction. You should go through this code, and see for yourself! The program below create a simulation of a sphere moving in uniform circular motion. The key part will be to get the direction of the ball’s acceleration correct.
The physics in the vPython program below is at the very beginning and towards the end. In the definitions at the top, I define the radius RING_RADIUS of the desired circular motion of the ball. This is also the radius of the ring as well, so if the ball leaves the ring, there is a problem! I also give the initial velocity of the ball, which we will use later. Towards the end, I create a sphere ball and an arrow velArr representing its velocity vector.
Notice that I did not specify how to update the ball’s position; that will be your job. The next few steps you will complete are to justify why the centripetal acceleration is chosen the way it is. You will go through a couple of incorrect choices, and see that they do not give motion at a constant speed in a circle.
First, let’s assume that the ball moves at a constant velocity. Remember that this means there is no acceleration. Change the code so that ball.pos is updated in the usual way using ball.velocity and the time interval DT. After you do this, make a guess about what the ball’s motion will look like. Then run the code.
If you ran the program (and you should), you’ll see that the ball moves off the ring in a straight line. Newton’s first law tells you that an object with no net force acting on it (and therefore no acceleration) will continue with a constant velocity. In other words, if there is no acceleration, the ball will move in a straight path at a constant speed. Remember that vectors such as velocity have both a magnitude (“speed” = “magnitude of velocity”) and a direction.
So we need to do something more sophisticated than a simple constant velocity. Our next guess is to use the acceleration magnitude
derived above. Since it always feels like this is a push outwards when you travel in a circle, let’s assume that this acceleration is always pointing away from the center of the circular path (which is hopefully the ring!). To give this direction, we use the unit vector \({\hat r}\), where the vector \({\vec r}\) is the position of the ball. Remember from Lesson 07 (vector magnitude and direction) that \({\hat r}\) always points in the direction of the vector \({\vec r}\), so this will be an outward pointing vector. Thus, our guess will be that the acceleration vector is given by
To program this, you will need to modify the ‘Update ball position’ section inside the while loop of the program so that it has the basic form
# Update ball position, velocity, acceleration
unitRadial = #####
ball.acceleration = #####
ball.pos = #####
ball.velocity = #####
First you have to define the vector unitRadial, and then use this to calculate the attribute ball.acceleration. Remember that unitRadial is the unit vector pointing from the origin to the ball, so you will use ball.pos (this is the vPython variable corresponding to the position \({\vec r}\)) and norm (to find the unit vector \({\hat r}\)). Then, using the vector unitRadial as well as the the magnitudes of ball.velocity and ball.pos, define ball.acceleration. After you do this, you need to update ball.pos, ball.velocity, and ball.acceleration inside the while loop. For ball.acceleration, you will use the same code to calculate it as you did above. This includes re-defining unitRadial, since the ball has moved. The other attributes ball.pos and ball.velocity must be updated as usual.
Once you have done all of this, run your modified program in the Trinket app. You should see that the ball still does not travel in a circle around the ring. In fact, it veers off away from the ring! The problem is that the acceleration has the right magnitude, but the wrong direction. The correct acceleration should be
In other words, the only change you need to make is to flip the direction of ball.acceleration by adding a minus sign. Change this where you calculate ball.acceleration, and then run your code.
This should give the proper motion – the ball moves along the ring at a (roughly) constant radius. Uniform circular motion only happens when the acceleration points towards the center of the circle. You “feel” an outward force not because there is one, but you are being forced from the outside inward by a net force. This net force is necessary to change the direction of your velocity, and overcome the tendency of inertial motion.
16.5. Centripetal force¶
16.5.1. How to keep things moving in a circle¶
As mentioned above, one of the big mistakes students make is to put the wrong direction for the centripetal acceleration. Hopefully, after working through the code above, you see why the direction is the way it is! There is a second big mistake that students make, dealing with the centripetal force. Let’s talk about that now.
You have seen that an object moves in uniform circular motion when there is an acceleration pointing towards the center of the circle with a magnitude of \(a_{cp} = v^2 / r\). By Newton’s second law, this tells us the direction of the net force acting on the object. Here is the key part: centripetal force is a new name for any net force moving in uniform circular motion. In other words, we are not introducting a new interaction, such as gravity, tension, or friction. Instead, we are collecting any and all forces that contribute to circular motion, and calling it the centripetal force. Note that some of the forces involved may actually “fight” this inward-pointing direction. For example, if you are riding a roller coaster at the bottom of a loop, the force of gravity points away from the loop’s center; only the fact that the normal force is larger, and pointing towards the center of the loop, keeps you moving along the track in circular motion.
Quantity: centripetal force
Symbol: \({\vec F}_{cp}\)
Equation: The centripetal force is “center-seeking”, i.e. always pointing towards the center of the circular motion. With the object at a position vector \({\vec r}\) (pointing from the center to the object), the direction of the centripetal force on the object comes from the unit vector \(-{\hat r}\), which points from the object to the center. Thus, the centripetal force is given by
Because centripetal force is just a special case of the net force, you will not put it on an FBD! Instead, you should draw the usual combination of forces that give the net force. The same is true of the centripetal acceleration, since we don’t put the acceleration on the FBD, either.
This new name for the net force in uniform circular motion means that Newton’s second law for objects moving in a circle will typically look like one of the equations below.
The \(\pm\) symbol in the equations is present because the net acceleration can be in the \(+\) or \(-\) direction.
16.5.2. An example: the tetherball¶
Let’s do an example to see how uniform circular motion arises from the centripetal acceleration. Suppose a 1.20 kg tetherball is swinging in a horizontal circle with a tangential speed at 15.0 mph, as shown in the picture below. The radius of the horizontal circle is 2.31 ft; the rope holding the ball in its path makes an unknown angle \(\theta\) with the vertical. We will find this angle \(\theta\), as well as the magnitude of the tension force the rope exerts on the tetherball.

Fig. 16.7 Tetherball moving in horizontal circle, attached to a string with angle \(\theta\) to the vertical¶
There are two forces acting on the ball – the tension force, and the gravitational force. Thus, the net force is
Before we start thinking about coordinates, it is useful to consider how the ball is staying in a circle. The vertical component of the tension is balanced by the ball’s weight, so there is no vertical acceleration. The ball is turning in a horizontal circle, however, so there must be a horizontal acceleration \({\vec a}_{cp}\) pointing towards the center of the circle. This means that there is a net force inward; only the horizontal component of the tension force can provide this. Since there is a non-zero horizontal acceleration, choosing the horizontal and vertical axes for our coordinates is probably the best bet.
With this in mind, the FBD of the ball looks like the diagram below.

Fig. 16.8 Free body diagram of the tetherball¶
The forces are broken up into their components as
Notice in particular the tension force components – \(\sin \theta\) goes with the \(x\) component, which is also negative to match the FBD and the original physical situation. This gives the Newton’s second law equations as
We go through the \(y\) component equation first. The ball is not accelerating up or down – it is maintaining the same vertical position, and not moving in a vertical circle – so \(a_y = 0\). Thus, we can solve for the tension force as
We don’t know the angle yet, though, so we need to use the \(x\) component equation as well. Here, there is an acceleration, since the tetherball is moving in a horizontal circle. Thus, the acceleration is the centripetal acceleration towards the center of the circle. This means it points to the left!
This gives the \(x\) force component equation as
If we cancel the minus signs, and substitute the tension force magnitude we got earlier, then we have
We can then solve for the angle \(\theta\) and get
Once we have this angle, we can find the magnitude of the tension force from the equation above. Plugging in the numbers gives \(\theta = 65.1^\circ\) and \(F_t = 27.9\) N.
Problem
An 11.8 kN car is rounding a flat circular curve of radius 45.0 m in the pictures below at a speed of 35.0 mph. What is the minimum coefficient of static friction needed between the tires and road so that the car navigates the circular curve safely?
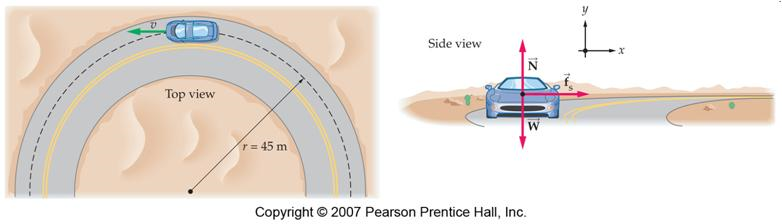
Fig. 16.9 Car on a flat curve with FBD¶
Answer: \(\mu_s = 0.554\)
Problem
A hammer thrower whose arms are 0.800 m in length is spinning around such that the hammer is traveling in a horizontal circle. If the ball is 8.25 kg, the (handle +) chain is 1.20 m in length and makes an angle of 15.0\(^\circ\) with respect to the horizontal, then:
What is the tension value (in N) in the chain?
How long does it take for the thrower to make one full revolution (in s)?
Answers: \(F_T = 313\) N; \(T = 1.47\) s
Problem
A pilot of mass 80.0 kg in a jet aircraft executes a loop-the-loop as shown below. In this maneuver, the aircraft moves in a vertical circle radius 2.57 km at a constant speed of 236 m/s.
What is the acceleration value (in m/s\(^2\)) of the pilot as the aircraft executes the loop-the-loop? What is this magnitude in terms of \(g\)?
What is the seat’s force (in N) on the pilot at the bottom of the loop?
What is the seat’s force (in N) on the pilot at the top of the loop?
Answers: \(a_{cp} = 21.7\) m/s\(^2\), or \(a_{cp} = 2.21 \ g\); \(F_{bot} = 2520\) N; \(F_{top} = 949\) N
Problem
Often, curves in the road will be banked at an angle to the horizontal, to allow cars to travel faster along the road without depending on friction. A curve in the road has a radius of \(R = 50.0\) m and the design speed is 35.0 mph. What angle would the road be banked at so that no frictional force is necessary to stay on the road? Hint: Think carefully about which coordinate axes you use!
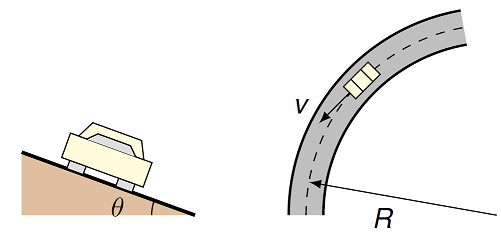
Fig. 16.12 Car on a banked curve¶
Answer: \(\theta = 26.5^\circ\)
16.6. Central forces¶
This is a good time to consider an important type of force we will see often in upcoming lessons; the gravitational, spring, and electrostatic forces are all members of this category. To set this up, suppose there is a special point which we will call the point \({\vec r} = {\vec 0}\) (the “origin” or “equilibrium point”), while an object at another point \({\vec r} \ne {\vec 0}\). Thus, the distance from the origin to the object is given as \(r\). Usually, this special point is not some abstract point, but instead corresponds to something physical. For the gravitational and electrostatic forces, \({\vec r} = {\vec 0}\) may correspond with another mass or charge that is affecting the motion of the object in question. For the spring force, where a spring is attached to the object, \({\vec r} = {\vec 0}\) is the location where the spring is neither compressed nor stretched.
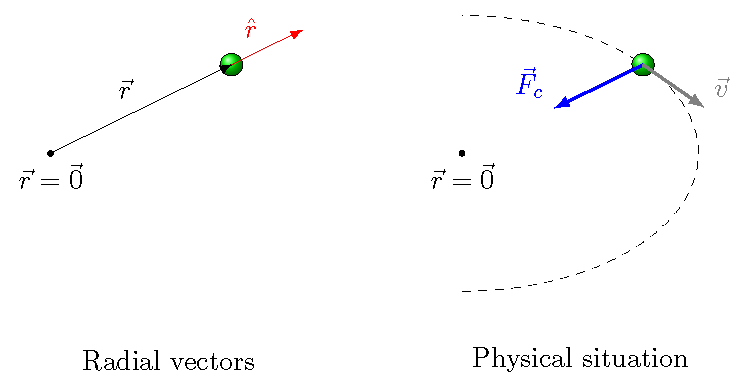
Fig. 16.13 The radial vectors and the physical situation for a central force¶
With this in mind, let’s now define a central force. A central force is a force \({\vec F}_c\) whose magnitude only on the value \(r\) – i.e. it does not depend on any angles. The direction of the force is either in the same or opposite direction as \({\vec r}\), the position vector of the object. In other words, a central force has the form
where \({\hat r}\) is the unit vector in the same direction as the position vector \({\vec r}\). Note that the function \(F(r)\) can be positive or negative. If \(F(r) < 0\), then the central force \({\vec F}_c\) points towards the origin, and the force is attractive towards that point. This is because the direction is opposite to \({\hat r}\), and \({\hat r}\) points away from the origin. On the other hand, if \(F(r) > 0\), then the central force \({\vec F}_c\) is repulsive, away from the origin. Note that some central forces can be either attractive or repulsive, depending on the objects involved! The best example is the electrostatic force, depending on whether the charges are the same sign (e.g. both positive) or different signs (positive and negative). We will see this again when we cover Coulomb’s law in Lesson 24.
Problem
Can an attractive central force give rise to uniform circular motion, for an object acted on by the force? What about a repulsive force?
Answer: Only an attractive central force can have uniform circular motion. As we saw earlier, whatever net force creates the centripetal force must point towards the origin, so this is not possible with a repulsive force.
Let’s now use the simplest version of a central force \({\vec F}_c\) possible, by making the magnitude \(F_c\) constant! Thus, we choose a constant force magnitude \(F_c\), and set
Problem
Suppose you place a ball at rest in the constant central force \({\vec F}_c\) given above, at a radius \(r\) away from the central point. What will the motion of the ball look like after it is placed at its initial position? Choose the best answer.
It will move in a circle around the central point at a constant speed.
It will move in a parabolic path around the central point.
It will remain at rest.
It will start accelerating away from the central point.
It will start accelerating towards the central point.
Answer: The ball will start accelerating towards the central point, due to the constant attractive force.
The program below simulates the motion of an object in a constant central force. If you run the program, you will see that the orbit does not immediately close, since the object does not return back to its starting point with the same velocity. Instead, the orbit is a complicated shape around the origin. This motion is explained in depth below the program.
So what is going on here with the ball’s motion? We can divide the velocity of the ball into two components: the radial velocity component \(v_r\), which is along the direction towards the origin, and the perpendicular velocity component \(v_\perp\), which is perpendicular to \({\vec r}\). Remember that, as the ball moves around the origin, the direction of the position vector \({\vec r}\) will change, and thus, so will what we mean by the \(v_r\) and \(v_\perp\) components. Now, everything we did above with centripetal acceleration dealt only with a constant speed \(v\). However, in this situation the ball is moving repeatedly moving closer, then further away, from \({\vec r} = 0\), so the speed will increase and decrease accordingly.
Remember how we are finding the new position and velocity, given the old ones. When we have the position \({\vec r}_n\) and velocity \({\vec v}_n\) at some time \(t_n = n \Delta t\), we can update the velocity using the acceleration \(a_n\) with the kinematic equation
to get the new velocity \({\vec v}_{n + 1}\) at time \(t_{n + 1} = (n + 1) \Delta t\). Now, uniform circular motion happens when this acceleration \({\vec a}_n\) is exactly the right value, so that the object stays on the circle, with the velocity \({\vec v}_{n + 1}\) tangent to the circle. This is shown below.
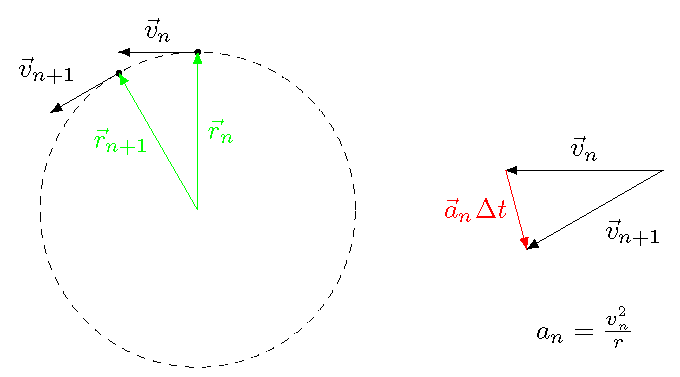
Fig. 16.14 Change in velocity when in uniform circular motion¶
Now what happens when the acceleration magnitude \(a_{n + 1}\) is either bigger or smaller than \(v^2 / r\)? These cases are shown in the figures below. When \(a_{n + 1} < v^2 / r\), then notice the angle between the old and new velocities \({\vec v}_n\) and \({\vec v}_{n + 1}\) is smaller than before. This results in the ball veering away from the center of the circle. The radius is getting larger, and the radial velocity component \(v_r\) is getting smaller, as the ball slows down. On the other hand, when \(a_{n + 1} > v^2 / r\), the angle between \({\vec v}_n\) and \({\vec v}_{n + 1}\) is bigger than when the ball was in uniform circular motion. The ball is getting closer to the center of the circle, and the radius is decreasing, while \(v_r\) is getting bigger.

Fig. 16.15 Velocity changes when acceleration is larger or smaller than \(a_{cp}\)¶
To see this in practice, look back at the graph accompanying the motion simulation. The blue line gives the object’s position \(r\) away from the origin as a function of time. As you saw when you ran the program above, the ball moves away from, then closer to, the center, over and over. This gives the cyclic motion you see in the blue line. Remember that this is only the radial motion; the ball also has a non-zero perpendicular velocity component \(v_\perp\) throughout its orbit, so it does not fall through the origin. The red line is more complicated – what it shows is the difference between the magnitude \(F_c\) of the central force, and the magnitude \(mv^2 /r\) of the centripetal force. In other words, it shows whether the acceleration magnitude \(a\) is larger or smaller than than the value \(v^2/r\) required to move in a circle with constant radius.
As we said above, when \(F_c < mv^2 / r\), the ball veers away from the center. So, in the graph, notice that when \(F_c - mv^2 / r < 0\), the ball’s motion towards the center slows down, then reverses to move away from the center. Remember that force changes velocity, not position, so there is not an instant change in radial motion when \(F_c - mv^2 / r < 0\)! On the flip side, when \(F_c - mv^2 / r > 0\), then the ball’s motion will start curving towards the center of the circle. So the radial component \(v_r\) of the ball, originally pointing outward, will decrease in size, then start pointing towards the origin.
Here is a helpful analogy. Suppose you are driving a car, and trying to make a tight turn. If the frictional force is large enough between the tires and the road, you can do this, and the car makes the required path of small radius. However, if your tires slip, or the road is icy, then you can’t make the turn, and your car will slip outward to a turn with a larger radius. This is what is happening every time the ball starts moving towards the center, due to the central force. The constant force \({\vec F}_c\) is insufficient to keep the ball in a tight circle, so the ball “slips” outward. Eventually, the radius is so large that the central force can start pulling the ball towards the origin, even as the ball continues to orbit this point.
Problem
Assuming an object of mass \(m\) is moving in a constant central force with magnitude \(F_c\), find an algebraic equation for the tangential speed \(v\) needed to keep the object moving in a circle of constant radius. Then, use the default values in the program above to find the numerical value of this speed, so that the mass (with size MASS in the program) orbits in a circle with radius INIT_POS due to a given force with magnitude FORCE_MAG.
Answer: The equation for the required tangential speed is
For the default values in the program, this gives \(v_t = 3.54\) m/s.
We will explore these ideas later, when we talk about the central forces of gravitation and the electrostatic force.
16.7. Summary¶
There are many situations where objects move in a circle, from a car driving around a turn, to the planets orbiting the Sun. This is due to an acceleration that has a constant magnitude, but a continually changing direction. We will build on these ideas in future lessons. The obvious case, mentioned at the beginning of this lesson, is the orbits of objects in space, due to the gravitational force (covered in Lesson 22). Another occurrence is looking at the motion of a mass on a spring, if the mass is “orbiting” as well, moving in an elliptical path. Both of these examples have a lot of similarities in their motion, and hopefully we will get a chance to discuss this a little.
We also started talking about central forces. We will see this idea several times again in the remainder of the course; some examples are gravitation, the spring force, and the electrostatic force. Central forces use many of the ideas we talk about in these lessons, so it will be a frequent example. In this lesson, we already saw how to define a central force in terms of an object’s position vector, and possible types of motion the object can have. This motion is described not only in terms of the tangential velocity component, but also its radial velocity component (towards or away from the center). Although we didn’t talk about it here, the tangential speed \(v_t\) actually changed as the ball moved in its orbit, an example of non-uniform circular motion. In this case, there is the centripetal acceleration talked about in this lesson, pointing towards the center of the circle, as well as a tangential acceleration pointing either in the same direction, or the opposite direction, to the motion. This might happen if you use the gas or brakes as you drive a car around a turn. We will revisit this when we talk about angular momentum in Lesson 18.
After today’s class, you should be able to:
Define centripetal acceleration, and state its direction.
Explain the relationship between inertia and “centrifugal force”.
Use Newton’s 2nd law for an object in uniform circular motion to find an unknown force.
Describe a central force.