.ipynb .pdf

Binder

Contents

10. Linear momentum and Newton’s laws of motion

10.1. Overview

Newton’s laws of motion form a crucial piece of physics, both historically and conceptually. We will be building a lot of what we do in this course on them, so it is important to make sure you understand these concepts! They deal with the relationship between “forces” and the acceleration of an object. Up to this point, the acceleration vector has been handed to you, and you can then use the kinematic equations to solve for the position and velocity of the object at any time. In vPython, we did the same thing, using updating methods based on average velocity and acceleration. But in all of these cases, the reason for a particular acceleration was perhaps mysterious. Newton’s laws of motion will allow us to calculate the acceleration of an object explicitly, based on its physical situation, and thus the forces acting on it.

This lesson will explore the laws of motion and their consequences, without worrying about specific forces. We will focus here on the observable consequences of Newton’s laws. For example, how can I see the effect of a force on a moving object? How do interactions between objects work? To do this, we will define the concept of “momentum”, which directly relates to the motion of an object; from there, forces will intuitively be things that change momentum. Starting with Lesson 12 (Solving force problems), we will begin to bring in specific forces – such as gravity, tension, friction, and the normal force – and look at how they affect the motion of objects.

Fig. 10.1 Roman copy in marble of a Greek bronze bust of Aristotle by Lysippos, c. 330 BC, with modern alabaster mantle. (source)

Early concepts of momentum were based on commentaries of Aristotle’s view that objects require a continual force to keep moving. In the 6th century, for example, Philoponus pointed out it did not make sense that objects were moved by the same air that resisted their motion.

Fig. 10.2 Portrait of René Descartes by Frans Hals (source)

In the 17th century, there was much controversy among physicists – there was a general sense of a quantity (generically called “force”) conserved during motion, but a lack of understanding of what it was. For example, Descartes argued for the quantity \(m|{\vec v}|\); notice this is a scalar quantity! On the other hand, Leibniz argued for \(mv^2\). The first evolved into linear momentum; the latter we will see later in Lesson 19 is twice the kinetic energy of an object.

Fig. 10.3 Sir Isaac Newton (source)

Newton is one of the greatest scientists in history, for developing (along with Gottfried Liebniz) calculus, and placing physics on a firm mathematical footing. He attended Cambridge University; while it was closed from 1665 to 1667 due to the Great Plague (social distancing!), he started developing his laws of motion, principles of optics, and a universal law of gravitation. In later years, he acted as Master of the Mint, taking responsibility for the coinage in England, and wrote many works dealing with interpretations of the Bible.

Through the late 1600’s and early 1700’s, there continued a confusion between “force” and “momentum”, including by Newton in his great work Principia, but the correct definition of momentum – as a quantity with direction – was in use by 1721, as seen in John Jennings’ textbook Miscellanea in Usum Juventutis Academicae.

Here are the objectives for this lesson:

• Define linear momentum and impulse.

• Calculate the impulse on an object after it interacts with another object.

• State Newton’s laws of motion.

• Calculate the average force acting on an object after it interacts with another object over a given time interval.

• Calculate the acceleration or final velocity of an object after it experiences a force over a given time interval.

10.2. Momentum and impulse

10.2.1. Definition of linear momentum

As we will see when we get into the actual laws of motion, objects have “inertia”. Inertia literally translates as “laziness”, and is the physical property of objects to continue their state of motion unless an interaction with other objects causes a change in this motion. This is a bit of a vague statement, so “linear momentum” is used to quantify this property. This is a quantity that is the simplest way to combine two facts: the objects we deal with have a mass, and these objects will continue with a constant velocity until outside forces combine to change this velocity. Thus, linear momentum \({\vec p}\) is defined as a vector with the same direction as velocity.

• Quantity: linear momentum

• Symbol: \({\vec p}\)

• Equation: \({\vec p} = m {\vec v}\)

• SI units: kg \(\cdot\) m/s

Thus, we can say that inertia corresponds to a constant linear momentum, and forces due to an interaction will change this momentum. Note that we tack on the adjective “linear” because we are dealing right now with things moving along a line. Later when we consider rotation, there will be a “angular” or “rotational” version of momentum, relating to the property of continuing rotational motion.

Problem

The SIG Sauer P226 has a rated muzzle speed of 335 m/s. If the bullet’s mass is 7.45 g FMJ, what is the magnitude of the bullet’s linear momentum? Choose the best answer below.

1. 2.50 kg\(\cdot\)m/s

2. 2.74 kg\(\cdot\)m/s

3. 25.0 kg\(\cdot\)m/s

4. 2.50 \(\times 10^3\) kg\(\cdot\)m/s

Answer: 2.50 kg\(\cdot\)m/s

Problem

In each of the five pictures below, a ball is moving to the right, and its position is shown at every second. The larger balls have twice the mass of the smaller balls. Rank each of the five situations based on the magnitude of the linear momentum for each ball.

Fig. 10.4 Rank the linear momentum magnitude of the balls

Answer: \(E > C > A = B > D\)

Problem

A 142 g baseball has a velocity of 100 mph at 10.0\(^\circ\) south of east. What is the \(y\) component of the baseball’s momentum? Choose the best answer below.

1. \(-14.2\) kg\(\cdot\)m/s

2. \(-1.10\) kg\(\cdot\)m/s

3. \(+1.10\) kg\(\cdot\)m/s

4. \(+6.25\) kg\(\cdot\)m/s

5. \(+14.2\) kg\(\cdot\)m/s

Answer: \(-1.10\) kg\(\cdot\)m/s

10.2.2. Impulse

We said earlier how forces are related to changes in momentum, so we give this quantity a special name: impulse.

• Quantity: impulse

• Symbol: \({\vec I}\)

• Equation: \({\vec I} = \Delta {\vec p} = {\vec p}_f - {\vec p}_i\)

• SI units: kg \(\cdot\) m/s

Note that momentum can change either because of a change in mass or velocity. Also, because velocity is a vector, this means that changing the direction (even if the speed is constant) gives an impulse! A car driving around a circular track at constant speed is continually changing its momentum; this will tell us later that there must be a force acting on the car to make this happen.

Problem

A 419 g racquetball is traveling at 20.0 m/s in the positive \(x\) direction. It hits a vertical wall and travels at 20.0 m/s in the negative \(x\) direction. What is the magnitude of the change in momentum for the racquetball? Choose the best answer below.

1. 0.00 kg\(\cdot\)m/s

2. 8.38 kg\(\cdot\)m/s

3. 16.8 kg\(\cdot\)m/s

4. 20.0 kg\(\cdot\)m/s

5. 40.0 kg\(\cdot\)m/s

Answer: 16.8 kg\(\cdot\)m/s

Problem

An object has an initial momentum \({\vec p}_i\) at \(t = 0\), and at a later time \(t = \Delta t\), has a different momentum \({\vec p}_f\). These vectors are shown as the left two vectors in the figure below. Note that the position of these vectors in the figure does not necessarily reflect the position of the object at these times. Which of the following choices best represents the object’s change in momentum during this time interval?

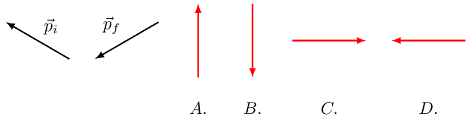
Fig. 10.5 What is the direction of the impulse for the given initial and final momentum vectors \({\vec p}_i\) and \({\vec p}_f\)?

Answer: \(B\)

Problem

A batter tries to hit a 95.0 mph fastball (initially traveling in the negative \(x\) direction), but fouls the ball straight up at a speed of 55.0 mph. The 145 g baseball is in contact with the bat for 1.50 ms. Calculate the magnitude of the impulse (in kg m/s) the bat delivers to the baseball.

Answer: 7.11 kg m/s

A bit of vocabulary that is used in physics: whenever I say normal, I mean a line or vector that is perpendicular to something else. Thus, a flagpole is normal to the ground; this is the sense of the normal in the diagram below being a “normal” to the wall shown.

Problem

The diagram below is a view from above of a squash ball with mass 24.0 g hitting the wall at an angle \(\theta\) of 30.0\(^\circ\) with respect to the normal. The ball hit the wall with a speed of 25.0 m/s and rebounded with the same speed and angle with respect to the normal (as shown). What was the impulse that the wall imparted on the ball as it rebounded? Find the magnitude in kg m/s, and the direction relative to the wall.

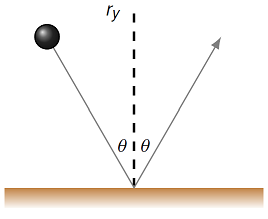
Fig. 10.6 Squash ball bouncing off of wall

Answer: 1.04 kg m/s, away from the wall

10.3. Forces

10.3.1. From momentum to force

We all have an inituitive idea of what a force is, based on our experiences in the natural world, although sometimes the effects of forces are confused with the “natural motion” of an object. For example, when we slide a book across a table, we expect that it will slow to a stop, so we may push it harder to get it to the opposite side of the table. Thinking in physics terms, though, it is not that books “want” to come to rest, but that there is a frictional force acting on the book preventing it from remaining at constant velocity.

That being said, let’s talk about the common properties of forces. Usually, forces are a push or a pull that can cause objects to change velocity (or accelerate). This can result in either a change in speed or direction, or both. Here are some common forces. One is the force \(F_g\) due to gravity, also know as the object’s weight. Near the surface of the Earth, \({\vec F}_g\) points directly downward. This force is given by

\[ {\vec F}_g = m{\vec g} \]

where \(m\) is mass and \({\vec g}\) is the gravitational field (with a magnitude of 9.81 m/s\(^2\) near the Earth). Another is the tension force \(F_T\), a force due to something like a rope or a string. The tension force acting on an object will point in the direction this connecting rope makes with the object at the point of contact.

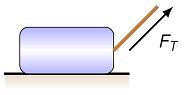
Fig. 10.7 Tension force due to a rope

Finally, the applied force \(F_{app}\) is a catch-all for forces due to interactions with people or other objects that cannot be explicitly calculated based on the object’s properties. An example would be you pushing a book across a table.

Fig. 10.8 Applied force acting on a block

Consistent labels for forces

We will always label forces with a capital \(F\), and a subscript indicating the specific type of force.

10.3.2. Newton’s zeroth law

Sometimes there are hidden assumptions that should be stated explicitly; here is an important one.

Newton’s zeroth law

An object at a particular instant responds only to the forces acting directly on it at that instant.

This idea will be crucial in determining which forces to include in the net force acting on an object. From experience, I notice that students intuitively understand this law when they are dealing with the motion of common objects – blocks sliding along floors or down ramps. It seems to be forgotten, however, when we start talking about gravitational or electrostatic forces between isolated objects. To show an example of what we will be doing later in the course, imagine that we have four masses arranged as shown in the figure below.

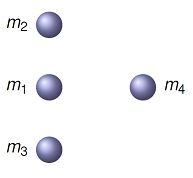
Fig. 10.9 Four isolated masses

These masses are isolated, so that there are no other objects nearby; if it helps, you can think of the objects as placed faraway in outer space. Now, when we talk about Newton’s universal law of gravitation, we will see that the net (gravitational) force on one object due to the others around it is found by adding all of the forces due to each of the other objects. This is known as the principle of superposition. In particular, there is a gravitational interaction between masses \(m_1\) and \(m_2\), which gives rise to a force \(F_{g, 12}\) on mass \(m_1\), and a force \(F_{g, 21}\) on mass \(m_2\). Notice how the subscripts change!. \(F_{ij}\) is the force on object \(i\) to due its interaction with object \(j\).

Now, suppose I wanted to find the net gravitational force acting on mass \(m_1\). What Newton’s zeroth law would say, along with the principle of superposition, is that I find the force on \(m_1\) due to each of the other three masses. I do not care about how the other masses are affecting each other – I don’t need to know what the force is between masses \(m_2\) and \(m_3\), for example. All I would need to calculate are the three forces due to \(m_1\) interacting with \(m_2, m_3\), and \(m_4\). For the other masses, I would do something similar: add up all the forces acting on that mass. This is the content of the zeroth law.

Problem

Three blocks are stacked as shown below. How many forces are acting on the bottom block \(m_3\)? Choose the best answer.

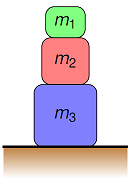
Fig. 10.10 Three blocks in a stack on the floor

1. one

2. two

3. three

4. four

5. five

Answer: There are three forces acting on the bottom block: the force of gravity (from the Earth), the contact force from the surface beneath, and the contact force with block \(m_2\).

10.3.3. Newton’s first law

Now let’s move on to the rest of the laws of motion. As we said above, inertia is the property of all objects to maintain a constant velocity; this would entail having a constant momentum. This law is stated:

Newton’s first law

An object will continue at a constant velocity unless acted on by an outside net (or total) force.

This includes an object at rest (\(\vec{v} = {\vec 0}\))! If an object is at rest or moving with constant velocity, then the sum of the net force on that object is zero, or \(\sum {\vec F} = {\vec 0}\). Remember that this is a vector equation, so we have to enforce zero total force along each of the three coordinate axes, or

\[ \sum F_x = 0 \quad \sum F_y = 0 \quad \sum F_z = 0 \]

Problem

Consider a cart on a horizontal frictionless table. Once the cart has been given a push and released, what will happen to the cart? Choose the best answer.

1. continue with constant acceleration

2. continue with constant velocity

3. continue with decreasing acceleration

4. immediately come to a stop

5. slowly come to a stop

Answer: The cart will continue with a constant velocity, since the net force on it is zero. Notice that there are forces acting on the cart, just that they all cancel out.

Problem

A hockey puck slides on ice at constant velocity. What is the net force acting on the puck? Choose the best answer.

1. more than its weight

2. equal to its weight

3. less than its weight, but more than zero

4. depends on the speed of the puck

5. zero

Answer: Since the puck is moving at constant velocity, the net force on it must be zero.

Problem

You put your book on the bus seat next to you. When the bus stops suddenly, the book slides forward off the seat. Why? Choose the best answer.

1. a net force acted on it

2. gravity briefly stopped acting on it

3. it did not move, but only seemed to

4. it remained at rest

5. no net force acted on it

Answer: When the bus is moving, the book has a constant velocity. The bus stops because a frictional force acts on it from the brakes; the book will continue moving, since it has no net force acting on it. The book will appear to start moving from your viewpoint, but that is because you are accelerating in the opposite direction!

10.3.4. Newton’s second law

Here we come to the workhorse for physics! We have seen before that an object’s constant velocity (or momentum) is altered by the application of a force to that object. Newton’s 2nd law tells us exactly how the momentum is changed. Thus, it provides the key relationship between the motion of a single object, and the interactions that object experiences, giving rise to a net force.

Newton’s second law

The change in the momentum \(\Delta {\vec p}\) of an object over a time interval \(\Delta t\) is equal to the net (or total) force acting on the object.

\[ {\vec F_{net}} = \sum {\vec F} = \frac{\Delta {\vec p}}{\Delta t} \]

Note that the net force vector and the change in momentum (or impulse) vector are in the same direction. For a single object, the mass is constant, so

\[ {\vec F_{net}} = \frac{\Delta (m {\vec v)}}{\Delta t} = m \biggl( \frac{\Delta {\vec v}}{\Delta t} \biggr) = m {\vec a} \]

Objects (e.g. rockets) with changing masses will be dealt with using Newton’s third law. This is the usual form of Newton’s 2nd law, and we will use it this way for most of the course. However, it is perhaps conceptually more helpful to think of the law as saying “forces change momentum”. This provides a more intuitive basis for both of these concepts.

Problem

In each of the four pictures below, a ball is moving to the right, and its position is shown at every second. There are no forces acting on the ball, except possibly at point \(P\).

1. In which of the four situations is a force acting on the ball at point \(P\)?

2. For the choices you made in the previous question, what is the direction of the force in each situation?

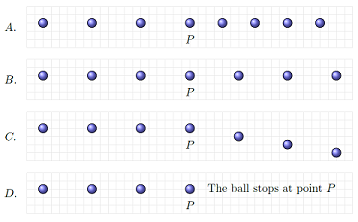
Fig. 10.11 Which of the balls shown have a force acting on them at point \(P\)?

Answers: All the balls experience a force at point \(P\), except in situation \(B\), where the ball continues with a constant velocity. For ball \(A\), the force is to the left, since the ball slows down (and thus, experiences a leftward acceleration). The situation is the same for ball \(D\), except that the leftward acceleration is larger, since the change in velocity is big enough to stop the ball. For ball \(C\), the force is towards the bottom of the page, since the velocity increases in that direction.

Whenever we have a problem dealing with forces on an object, Newton’s 2nd law is frequently the first mathematical tool we will pick up out of the toolbox. Even in cases, such as energy conservation, where we do not directly see these equations, it will be “in the background”, providing the conceptual framework to define quantities such as potential energy. You should get into the habit of starting your solutions to problems with Newton’s 2nd law!

Problem

A disorganized group of people are trying to move a stalled car. Two people are trying to pull it forward with 100. N and 150. N each, while one is trying to pull it backwards with 200. N. If the car has a mass of 1500 kg, what is the acceleration of the car? Choose the best answer below.

1. zero

2. 3.33 cm/s\(^2\), backward

3. 3.33 cm/s\(^2\), forward

4. 10.0 cm/s\(^2\), backward

5. 10.0 cm/s\(^2\), forward

Answer: 3.33 cm/s\(^2\), forward

Problem

You work at an engineering firm, testing the safety of car components under large accelerations. When testing a particular 175 g piece of equipment, you find the following \(v_x\) vs. time graph. What is the average force (in N) on the equipment from 1.00 ms to 5.00 ms? Give your answer in unit vector form.

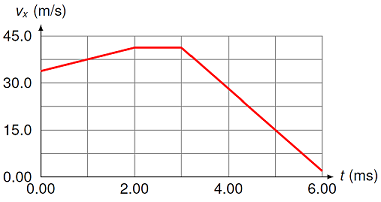
Fig. 10.12 Measuring the velocity of a car component as a function of time

Answer: \({\vec F}_{avg} = (-984 \textrm{ N}) {\hat x}\)

Problem

A hockey puck with a mass of 155 g is hit with a force with magnitude \(F\). The force causes the puck to accelerate from 15.0 m/s to 25.0 m/s in 1.79 s. What is the magnitude \(F\)? Choose the best answer below.

1. 866 mN

2. 1.59 N

3. 2.17 N

4. 3.88 N

5. 4.94 N

Answer: 866 mN

Problem

A cart is pulled with a constant, horizontal net force of 110 N. The cart starts from rest and reaches a speed of 9.50 m/s over a distance of 15.5 m.

1. How long does it take (in s) for the car to reach its final speed?

2. What is the mass of the cart (in kg)?

Answers: 3.26 s; 37.8 kg

Problem

You are driving in your 1000 kg car with an initial velocity \((25.0 \textrm{ m/s}) {\hat x} + (15.0 \textrm{ m/s}) {\hat y}\) when you encounter a bend in the road. You brake and turn, ending up with a final velocity \((10.0 \textrm{ m/s}) {\hat x} + (18.0 \textrm{ m/s}) {\hat y}\). If you turned in 2.23 seconds, what is the net force (in kN) acting on the car?

Answer: \({\vec F} = (-6.73 \textrm{ kN}) {\hat x} + (1.35 \textrm{ kN}) {\hat y}\)

10.3.5. Newton’s third law

As said above, Newton’s 2nd law will be our go-to source for finding how interactions on a single object change its momentum. But what are the sources of these interactions? Where are the forces coming from? These questions naturally lead to thinking about how a given object is effected by the other objects around it. Newton’s 3rd law describes an crucial property that these interactions must have.

The important thing to realize is that a force on one object cannot happen unless it is due to an interaction with a second object. An object will not start moving because of a force acting on itself! Two objects share the interaction we call a “force”. This force of interaction acts with equal size on both objects. Only because of Newton’s 2nd law will these forces generate different accelerations, because of the differing masses of the objects. The directions of the forces must also be in opposite directions – they can’t “add up”, or else you get extra acceleration for free! The forces of the interaction do not cancel out, because they act on different objects. Putting all of this together gives

Newton’s third law

Two interacting objects will each feel the same magnitude of force due to this interaction, acting in opposite directions.

As we said before, let \({\vec F}_{AB}\) be the force on \(A\) due to \(B\), and similarly, \({\vec F}_{BA}\) is the force on \(B\) due to \(A\). Then the mathematical form of Newton’s third law is

\[ {\vec F}_{AB} = - {\vec F}_{BA} \]

Problem

A small car collides with a large truck. Which experiences the greater magnitude of impact force?

Fig. 10.13 A car and a truck, about to collide

1. the car

2. the truck

3. both the same

4. it depends on the mass of each

5. it depends on the velocity of each

Answer: Using Newton’s third law, the magnitudes of the forces are equal on the car and truck.

Problem

In the collision between the small car and the large truck, which has the greater acceleration magnitude?

1. the car

2. the truck

3. both the same

4. it depends on the collision time

5. it depends on the velocity of each

Answer: From the previous question, we know the force magnitudes are equal. Then, using Newton’s second law, the acceleration of the car is greater.

These last two questions focus on a frequent confusion. The first question – about the size of the force – is dealt with by Newton’s 3rd law. This law of motion pertains to the interaction between two objects, and says that this interaction must treat each object equally. However, this notion of equality does not say anything about how the interaction affects the motion of the individual objects. This is the content of Newton’s 2nd law, which relates the forces on an object to the resulting change in the object’s motion. Thus, the second question – about the size of the acceleration – starts with what Newton’s 3rd law says about interactions, and uses it as input for Newton’s 2nd law. You need to use Newton’s 3rd law to be able to say anything with the 2rd law!

10.3.6. Internal and external forces

Let’s explore another crucial implication of Newton’s 3rd law. Suppose a system is made of two objects \(A\) and \(B\). The rest of the universe is called the “outside” or “external” to the system. There are three possible forces acting on the objects: a force between \(A\) and \(B\) (\({\vec F}_{AB} = -{\vec F}_{BA}\)), a force between \(A\) and the outside (\({\vec F}_{A, out}\)), and a force between \(B\) and the outside (\({\vec F}_{B, out}\)). What is the net force on the system? It is the sum of the forces on all objects in the system:

\[ \sum {\vec F}_{sys} = \sum {\vec F}_A + \sum {\vec F}_B = \bigl( {\vec F}_{AB} + {\vec F}_{A, out} \bigr) + \bigl( {\vec F}_{BA} + {\vec F}_{B, out} \bigr) \]

Because of Newton’s 3rd law, \({\vec F}_{AB} + {\vec F}_{BA} = {\vec 0}\) as vectors for the system, not a single object. So

\[ \sum {\vec F}_{sys} = {\vec F}_{A, out} + {\vec F}_{B, out} = \sum {\vec F}_{sys, out} \]

The net force on a general system is thus the sum of all external forces acting on the system. Internal forces do not contribute to the motion of the system, but do affect the motion of the individual objects within the system. Be careful about the difference – for example, you do not start moving because your lungs expand with air as you breath! We will discuss “the motion of the system” again in Lesson 11 (center of mass).

It is important to know what system to look at when working with Newton’s second law. So let’s go through an example of this, where I consider the motion of a 1500 kg truck pulling a 500. kg sled along. The sled is on runners, so there is no friction between the sled and the road. The sled pulls on the truck with a force of 250. N to the left. The force of friction between the road and the truck’s tires is 1000 N.

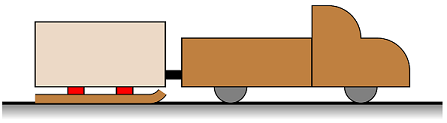
Fig. 10.14 Truck and sled

We will figure out the accelerations of the truck and the sled, the force of the truck on the sled, and the net force on the truck. Because I have two objects interacting, I can divide them in two ways: either as individual systems, or as a combined system. Depending on which system I consider, there will be different forces acting on the system. These are shown in the figure below.

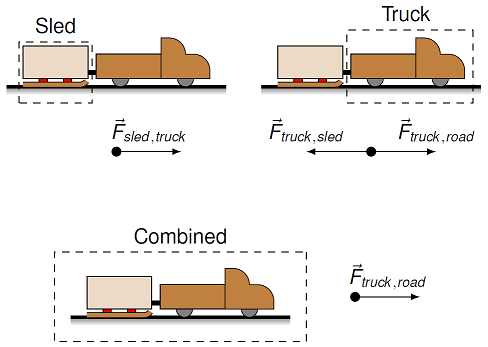
Fig. 10.15 The forces on the truck and sled as individual objects, and as a system

For the sled, with no friction, the only external force is the force on the sled, due to the truck. For the truck, there are two external forces: the force on the truck, from the road (i.e. friction), and the force on the truck due to the sled. If I look at the combined system, the only external force is the force on the truck due to the road. In this last case, the internal forces are those between the truck and the sled. These internal forces only cancel out inside the system due to Newton’s 3rd law. So it is important to think about what system you are using! Forces from outside the system do not cancel. The diagram below considers the three possible systems we can make out of the truck and sled.

Notice that in the diagram above, I have also drawn diagrams to indicate the forces acting on each system. This type of diagram is known as a free body diagram (or FBD), and is a compact and effective way of showing all the forces. We will see many of these starting in Lesson 12 (Solving force problems), where I will go into them in more detail. For now, notice how I have drawn them:

1. A dot represents the system acted on by the forces.

2. Every arrow indicating a force points away from the dot.

3. Only forces are included; velocity and acceleration are not indicated on an FBD.

Now back to the problem. It is easiest to find the acceleration magnitude of the truck and the sled. To do this, we look at the combined system, since we know the size of the net force on it (1000 N), and the mass of the system (2000 kg). Using Newton’s 2nd law for this, we get an acceleration of 0.500 m/s\(^2\) to the right. Note this is the acceleration of both truck and sled, since they are attached – they move together as one unit.

Turning to the forces, since these deal with the forces between the sled and truck, we cannot use the combined system. We need to look at each object individually. To find the force between the sled and the truck, it is somewhat easier to use the sled. We know the mass of the sled, its acceleration, and the net force is simply the force on the sled due to the truck. Putting all of this together gives this force is 250. N to the right. Finally, we know from Newton’s third law that the truck experiences a force \({\vec F}_{truck, sled}\) of 250. N to the left from the sled. Since the net force on the truck is simply the sum of the forces acting on it, we get

\[ \sum F_x = -F_{truck, sled} + F_{truck, road} \]

Here, I am only writing the \(x\) components of the vector equation, so these are magnitudes, with signs giving the directions. Solving this equation for the net force \(\sum F_x\) gives 750. N, to the right. This is the same answer I get if, instead, I use Newton’s 2nd law and write

\[ \sum F_x = m_{truck} a_x \]

The next two problems deal with the interplay between forces on the system, and forces on the individual objects. Obviously, when solving for a particular force between the objects, it will be best to use Newton’s 2nd law, written down for one of the objects involved. As some problem-solving hints, you should draw a FBD for every system that you are considering. Remember that Newton’s 3rd law says that forces represent an interaction between two objects, so what you know may guide you in choosing one of the affected objects over the other. However, there are other quantities that are more easily found when looking at the system. These will be those that every object has in common.

Problem

On NAPS I-Day, you push three boxes of your favorite books into your room in Ripley. You exert a force \(F\) of magnitude 11.0 N on the three boxes \(m_1 = 1.90\) kg, \(m_2 = 4.20\) kg and \(m_3 = 3.30\) kg.

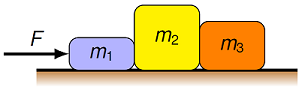
Fig. 10.16 Pushing three boxes of books into your room

1. What is the magnitude of the acceleration (in m/s\(^2\)) of the three boxes?

2. What is the magnitude of the force (in N) between boxes 2 and 3?

3. What is the magnitude of the force (in N) between boxes 1 and 2?

Answers: 1.17 m/s\(^2\); 3.86 N; 8.78 N

Problem

On your last day at NAPS, you line up the boxes in the same order, but now you exert the same force \(F\) of magnitude 11.0 N on the right hand side. Remember that \(m_1 = 1.90\) kg, \(m_2 = 4.20\) kg and \(m_3 = 3.30\) kg.

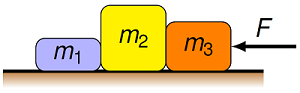
Fig. 10.17 Pushing three boxes of books out of your room

1. What is the magnitude of the force (in N) between boxes 2 and 3?

2. What is the magnitude of the force (in N) between boxes 1 and 2?

Answers: 7.14 N; 2.22 N

10.4. Summary

It is not too far off to say that Isaac Newton, when he presented his ideas in Principia, created the first unified system of mathematical physics. Not only did he provide a rigorous framework for investigating the natural world, but he also linked all phenomena known at the time into a single picture. Obviously, much has been discovered since that time, but the core ideas of Newton still provide the skeleton on which our understanding of the Universe sits. This core is summed up in Newton’s laws of motion. Understanding their consequences took the effort of many physicists and mathematicians over many decades.

After this lesson, you should be able to:

• Define linear momentum and impulse.

• Find the impulse of an object due to a change in velocity.

• State Newton’s laws of motion.

• Define inertia.

• Calculate the final velocity or acceleration of an object, knowing its mass, initial velocity and the net force acting on it.

• Define an isolated system.

• Describe the net force acting on an isolated system.

• Calculate the acceleration of an isolated system, or the internal forces between objects in that system, given the appropriate information.

9. Relative motion 11. Center of mass and collisions