14. Inclined planes¶
14.1. Overview¶
Links to programs in this lesson:
Everyone has heard of the famous experiment where Galileo Galilei dropped two masses off the top of the Leaning Tower of Pisa, in order to show that the force of gravity accelerated all objects equally. Unfortunately, this story is probably not true! What he did instead is more interesting, and leads to actual mathematical relationships dealing with acceleration and gravity. His experiment is a prime example of how the inclined planes we will discuss in this lesson were important to our greater understanding of physics. As described in the video linked below, he rolled a ball down a groove at an angle to the horizontal, and saw how the ball would accelerate.
We will study this example, and others like it. In this lesson, there will be the conjunction of several topics we have talked about before: the scalar product, Newton’s laws of motion, and the gravitational, frictional, and normal forces. As detailed before, the scalar product allows us to divide a vector into pieces along a set of directions. However, instead of the usual “horizontal” and “vertical” directions (or \(x, y\), and \(z\) axes), we will use the directions “parallel” and “perpendicular” to the ramp or incline. This, along with Newton’s 2nd law, allows us to find the equation of motion for an object moving along the ramp. There will always be a gravitational force, and the normal force due to the ramp itself; there will also be the possibility of a frictional force from the interaction between the object and the inclined plane.
Here are the objectives for this lesson.
Define the normal force.
Write down the Newton’s 2nd law equations for an object on an inclined plane.
Explain how the parallel and perpendicular components of the gravitational force acting on an object on an inclined plane change in size as the ramp angle changes.
Solve for the acceleration of an object on a frictionless inclined plane.
Use unit vectors to define the acceleration for an object on an inclined plane.
14.2. From horizontal to inclined surfaces¶
We now have enough mathematical and conceptual tools to look at objects moving along a ramp or incline. Below is a brief description of how we will go about this. In Lesson 11 (scalar product), we defined the scalar product between two vectors. Then we showed that one useful property it had was identifying vectors that were perpendicular to each other. In this lesson, we will put this into practice by defining two unit vectors along a surface – one vector \({\vec e}_{||}\) will be parallel to the surface, and the other unit vector \({\vec e}_\perp\) will be perpendicular to the surface. Since, in general, objects on an inclined plane move along the surface, the motion should be written solely in terms of the parallel unit vector \({\vec e}_{||}\).
The game plan for this lesson will be the following. First, we will revisit the motion of an object along a horizontal surface. We are used to thinking of this in terms of the unit vectors \({\hat x}\) and \({\hat y}\), i.e. “horizontal” and “vertical”. However, it will help us later to rewrite these as two unit vectors that are parallel and perpendicular to the horizontal surface. After we have done that, then we are ready to consider inclined planes. Instead of having a horizontal surface, the surface will now be at an angle \(\theta\) to the horizontal. This will change the definitions of our parallel and perpendicular unit vectors \({\vec e}_{||}\) and \({\vec e}_\perp\), as well as some of the force vector components in terms of them.
Suppose the block is acting on by an applied force pointing at an angle, as shown in the diagram below. Because the block is sitting on a surface, it will have a normal force \({\vec F}_N\) acting on it, as well as the gravitational and applied forces.
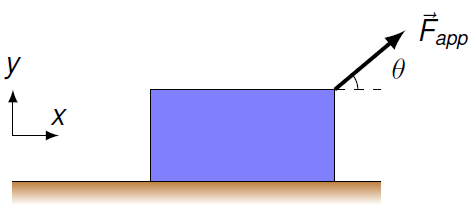
Fig. 14.1 Block moving along a horizontal surface¶
The net force equation, as a vector equation, is given by
where
Before now, we would “strip off” the \(x\) and \(y\) components of the Newton’s 2nd law equation above, and solve them separately. However, we can now do this process more formally using the scalar product; it will help you later to start thinking it these terms, for when we start looking at things moving on ramps. For the case at the moment, the block on the horizontal ground, the usual force component equations can be found using the scalar product:
At this point, using Newton’s 2nd law, the forces in the \(x\) and \(y\) directions would be set equal to the accelerations in the respective directions. Remember that \(a_x = {\vec a} \cdot {\hat x}\) and \(a_y = {\vec a} \cdot {\hat y}\), giving the equations
Now, suppose we look at an object sliding down an inclined plane. In general, there will be three forces acting on the object – gravity, the normal force, and the force of friction (up the ramp, since the object moves down the ramp). There may be additional forces as well, such as a tension force from a rope, or some other applied force. At the moment, we will not worry too much about any forces except the gravitational and normal forces, but you should keep them in the back of your mind for when we do start adding them in.
Problem
Suppose you have a stationary block on an inclined plane as shown in the diagram below. This block is acted on by the force of gravity, the normal force, and the force of friction. What would the resulting FBD look like?
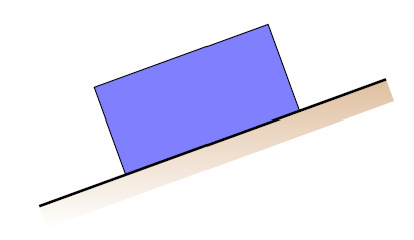
Fig. 14.2 Block on an inclined plane¶
Answer: Here is an example of what the block’s FBD should look like; we will see later in the lesson how you might want to add coordinate axes and an angle \(\theta\).
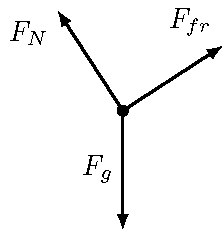
Fig. 14.3 FBD for block on an inclined plane¶
Two out of three of the forces mentioned in the problem above have components in the \(x\) and \(y\) directions. In addition, the acceleration would also have both \(x\) and \(y\) components – both \(a_x\) and \(a_y\) are not zero. This makes things complicated!
Instead of \({\hat x}\) and \({\hat y}\), it is more useful to define two new unit vectors: a vector that is parallel to the surface of the ramp (\({\hat e}_{||}\)) and one that is perpendicular to the ramp (\({\hat e}_\perp\)).
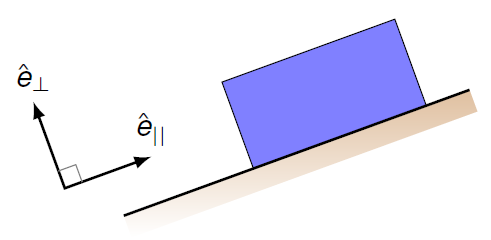
Fig. 14.4 Block on inclined plane, with parallel and perpendicular directions labeled¶
What will be the unit vector \({\hat e}_{||}\) along the ramp? It must have a magnitude of 1, and point at an angle of \(\theta\) above the \(+x\) axis (for the picture above). Thus, it must be equal to
Problem
Verify that this definition makes sense to you. Which way would the unit vector \({\hat e}_{||}\) point if the ramp was flat (\(\theta = 0.00^\circ\))? If the ramp were straight up (\(\theta = 90.0^\circ\))?
Answer: If the ramp was flat, then \({\hat e}_{||}\) would be the same as \({\hat x}\), and point horizontally. If the ramp was oriented straight up, then \({\hat e}_{||}\) is equal to \({\hat y}\), pointing vertically.
Can you see what \({\hat e}_\perp\) must be equal to? Since \({\hat e}_{||} \cdot {\hat e}_\perp = 0\), then one possibility \({\hat e}_\perp = (-\sin \theta) {\hat x} + (\cos \theta) {\hat y}\). This is the choice we will use in this lesson.
Problem
The vector \((\sin \theta) {\hat x} + (-\cos \theta) {\hat y}\) also has a zero scalar product with \({\hat e}_{||}\). So why are we not using that choice?
Answer: This choice of vector points into the ramp; when the ramp is flat, this would be the same as the unit vector \(-{\hat y}\). Thus, it would not match up with how we worked through previous problems on flat surfaces.
Our next step could be to now write out Newton’s 2nd law vector equation, then take the scalar product of it with \({\hat e}_\perp\) and \({\hat e}_{||}\) to get two component equations. However, before we do that, let’s motivate how the normal force is related to the gravitational force by trying different choices in vPython. We will see that there is a specific relation needed between the two to get an object to slide along the surface exactly.
14.3. Creating an inclined plane in vPython¶
We start below with code that creates a block in the center of a horizontal surface. You will gradually update this code, until it gives you a block on an inclined plane. How to do this is described after the program given below. This program has a function creating a ramp with a block on it. Since this is an “initialization” function, we call it init(). When you run the program below, it uses this function to put the block on the ramp. To start with, the block and ramp are horizontal; you will add the code needed to have both the ramp and block tilt at the desired angle. The function init() only returns the object block, since the ramp will be stationary for the entire simulation; only the block will (eventually) change position. Verify that it works as you expect.
Next, we are going to modify the program above, so that it is written in terms of unit vectors parallel and perpendicular to the surface. As discussed above, the ramp and the block should point along the parallel unit vector \({\hat e}_{||}\), given by
In vPython, using Q for \(\theta\), this vector would be
unitPar = vector(cos(radians(Q)), sin(radians(Q)), 0)
We will define the angle Q in degrees, for ease of understanding. However, the vPython functions sin and cos work with radians. The radians function must be used to convert to radians, so the cos and sin functions give the correct answer.
At this point, the computer does not know what angle to use. We want everything to remain horizontal for the moment, so define the ramp angle as zero:
Q = 0 # Ramp angle, in degrees
Copy these definitions into the “Constants and definitions” section in the original Trinket app above. You should put your definition of unitPar after the definition of Q, so that the computer knows what the value of that variable is! Then use this to define ramp.axis and block.axis by adding the code axis = unitPar inside the parentheses for the definitions of ramp and block. If you remember when you dealt with arrow objects, the axis attribute tells the computer which way the arrow is to point. The box object also has an axis attribute, which tells the computer which direction the \(x\) axis of the box should point.
Run the program. If you have done everything correctly, nothing should change! Our definitions of parallel and perpendicular unit vectors include the usual \({\hat x}\) and \({\hat y}\) unit vectors. But they can do much more – redefine the ramp angle to \(30.0^\circ\), i.e. change the program above so that Q is defined like
Q = 30 # Ramp angle, in degrees
Run the program again; the ramp and block should both be rotated to an angle of \(30^\circ\) above the horizontal.
14.4. Inclined planes and forces¶
You will now built up the proper forces acting on the block sitting on the ramp. I often see students make mistakes with which forces to use, and what magnitude to give them. Thus, I want you to see some examples of bad choices, so it is obvious why the choices are bad.
Thus, before we get into the proper way of solving for the forces, let’s try to make some guesses about what the size and directions of these forces would be. The program below uses the init() function you defined earlier, so make sure that it includes a proper inclined plane. The usual evolution loop has been added at the end, with the accompanying definitions for the time. However, at the moment, the net force is set to zero, which is definitely not true when there is no friction!
To make sure you know where to put the code, I will say the main procedure when I refer to the part of the program after the definition of init(), i.e. after the command return block.
Now that the basic set-up of the ramp and block are complete, it is time to add in the motion of the block down the ramp. You will do this by gradually adding forces to the system. The key point will be that the normal force of the ramp acting on the block must have a certain size and direction, or else the block will not slide exactly down the ramp.
Let’s first add in the force of gravity. Add the definition of the gravitational field \({\vec g}\),
GRAV_FIELD = vector(0, -9.81, 0) # in m/s^2
to the “Constants and definitions” section of the program for init() above. Then define the net force block.force in terms of the force of gravity \({\vec F}_g = m{\vec g}\). Now, run the program with the main procedure. What kind of motion do you see?
The block should fall straight downward, as if the ramp wasn’t there! Obviously, this is wrong, and the ramp is exerting a force to prevent this from happening. Remember this is known as the normal force \({\vec F}_N\). So we need to add this in as well. This force has to balance the force of gravity, so let’s guess that the two are the same magnitude, but the normal force points perpendicular to the ramp. This means we need to define the perpendicular unit vector \({\hat e}_\perp\). Based on what we talked about previously, in vPython, this would be
unitPerp = vector(-sin(radians(Q)), cos(radians(Q)), 0)
Add this into the “Constants and definitions” section of init(), right after the definition of unitPar, then change the net force block.force there so that it reads what we just guessed:
block.force = block.mass * GRAV_FIELD + mag(block.mass * GRAV_FIELD) * unitPerp
The second term is our guess for the normal force, with magnitude \(mg\), and direction \({\hat e}_\perp\). Run the main procedure now, and see if this works as you expect.
Turns out that it still doesn’t work – the block slides down the ramp, but it levitates at the same time! Since it is going off the ramp now, this means the normal force we are using is too big.
Let’s go through this properly, by looking at how the physics would change for an inclined plane, and see what the magnitude of the normal force should be in this situation. The diagram has a block on an inclined plane, with only the gravitational and normal forces acting on it.
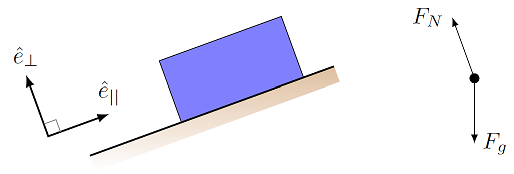
Fig. 14.5 Block on inclined plane and its FBD¶
The normal force is what it needs to be
There is no set equation for the normal force. This force will be whatever value is neccessary to prevent objects from going through each other. To find the magnitude of the normal force, in every case you must go through Newton’s 2nd law, and solve for \(F_N\).
The resulting vector equation for Newton’s 2nd law is given by
We shall go through and solve this equation for the normal force acting on a block moving along an inclined plane. We do this by breaking up the vectors into their parallel and perpendicular parts using \({\hat e}_{||}\) and \({\hat e}_\perp\).
Since the acceleration only points down along the ramp, with \({\vec a} = (-a) {\hat e}_{||}\), then it will be convenient to use the two equations
Why I chose these axes
Remember that we are using the choice of parallel and perpendicular (instead of \({\hat x}\) and \({\hat y}\)) since (1) the acceleration points along the parallel direction, and (2) it makes the equations easier. However, there are cases where the acceleration is not solely parallel! We will see these when we talk about circular motion in Lesson 16.
We first write the forces in terms of \({\hat x}\) and \({\hat y}\) as
Then we can use our definitions of \({\hat e}_{||}\) and \({\hat e}_\perp\) to give
and therefore
Problem
A farm tractor tows a 3700 kg trailer up an 18.0\(^\circ\) incline with a steady speed of 3.20 m/s.
What force value (in kN) does the tractor exert on the trailer?
What is the magnitude of the normal force (in kN) acting on the trailer?
Answers: 11.2 kN; 34.5 kN
Challenge
Do the same Newton’s 2nd law analysis we just completed, but use the unit vectors \({\hat x}, {\hat y}\) instead. Is \(a_y\) zero on the ramp? Which equations look simpler to use?
So the issue was that our normal force should only balance out the gravitational force in the perpendicular direction. To spell this out, from Newton’s second law above, we have
The fact that the acceleration is all along the parallel direction, so \({\vec a} \cdot {\hat e}_\perp = 0\), gives that the magnitude \(F_N = {\vec F}_N \cdot {\hat e}_\perp\) is
Putting this magnitude together with the unit vector \({\hat e}_\perp\) gives the code
block.force = block.mass * GRAV_FIELD - dot(block.mass * GRAV_FIELD, unitPerp) * unitPerp
Make this change in init(), and run the main procedure. The block should now slide right down along the ramp! Change the value of Q to other angles, and verify that this is the proper acceleration for any ramp angle \(0^\circ \le \theta < 90^\circ\).
Challenge
In the equations above, we saw that the parallel force component was \(F_{||} = -mg \sin \theta\). Show algebraically that the force vector \((-mg) {\hat y} + (mg \cos \theta) {\vec e}_\perp\) is equivalent to the vector \((-mg \sin \theta) {\hat e}_{||}\). This gives an acceleration of size \(g \sin \theta\) pointing directly down the ramp.
14.5. An example: Adding an applied force¶
Let’s mix things up a little, and consider an object moving on a ramp, with an applied force acting on it.
Suppose a shopper pushes a 7.50 kg shopping cart up a smooth 13.0\(^\circ\) incline, such that the acceleration of the cart is 1.41 m/s\(^2\) up the ramp. Ths shopper pushes the cart horizontally with an applied force of unknown magnitude. We are going to find the value of this applied force, and calculate the normal force as well. Note that we expect this normal force is larger than \(mg \cos \theta\), since the shopper is pushing the cart horizontally, and therefore into the ramp.
As always, we start with a FBD for the object in question, the shopping cart; this is shown below. The parallel and perpendicular axes have been marked on the FBD.
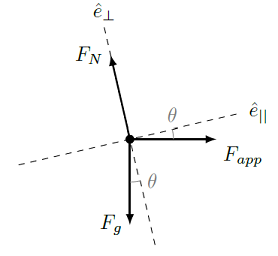
Fig. 14.8 The free-body diagram for the shopping cart¶
So, Newton’s 2nd law equation is
It is worthwhile to talk a little about why we are using the parallel and perpendicular directions for our axes, rather than the horizontal and vertical ones. After all, \({\vec F}_g\) points along the \(-y\) axis, and \({\vec F}_{app}\) points along the \(+x\) axis. However, there is a non-zero acceleration, pointing along \({\hat e}_{||}\). Thus, it is beneficial to use \({\hat e}_{||}\) and \({\hat e}_\perp\), so that one of the force component equations sums to zero. This will make the mathematics more convenient, even though it means we need to break both \({\vec F}_g\) and \({\vec F}_{app}\) into components. Let’s do that now, using the angles shown in the FBD. \({\vec F}_{app}\) is along the horizontal, while \({\hat e}_{||}\) is along the ramp, which has an angle \(\theta = 13.0^\circ\) to the horizontal. Similarly, as discussed above, \({\vec F}_g\) is an angle \(\theta\) away from the axis given by \(-{\hat e}_\perp\). This means that these two vectors are given by
Note that the perpendicular part of \({\vec F}_{app}\) is negative, since it points into the ramp. The component equations for Newton’s 2nd law are now
and
We can solve the first equation for the applied force magnitude \(F_{app}\). This gives
In this case, the acceleration is up the ramp, so \(a_{||} = +1.41\) m/s\(^2\). Substituting the values gives \(F_{app} = 27.8\) N. Once we have this, we can solve the second force component equation for the magnitude of the normal force,
Using the other values, this gives \(F_N = 78.0\) N.
14.6. Graphing the motion¶
Now that we have a good physical simulation for the motion of a block down a ramp, we can start graphing the position and velocity of the block. At this point, your code for init() and the main procedure should look like that in the program below. I have increased the height of the app window, so you can see the block’s motion and the accompanying graph at the same time, after you complete the code. Remember you can edit the code by clicking on the pencil icon at the upper-left corner of the app.
You will now create a graph of the block’s velocity component parallel to the ramp as a function of time. In the part of the main procedure code entitled “Create velocity graph”, first create a new graph velGraph, with the horizontal values running from 0 to MAX_TIME. If you wish, you can use the numbers in the code and calculate the final parallel velocity component of the block, and use that as your value of ymin (since it will be negative). Give the horizontal and vertical axes the labels “Time (s)” and “v_|| (m/s)”, respectively. Then create a curve velParCurve using this new graph velGraph; pick your favorite color for the line! If you do not remember how to do this, look back at previous lessons, such as Lesson 03 (velocity and the Euler method).
In the part of the main procedure labeled “Update velocity graph”, you will be graphing the part of the velocity that is parallel to the ramp. You can find this using the scalar product. In particular, you want to graph \(v_{||} = {\vec v} \cdot {\hat e}_{||}\), where \({\vec v}\) is the block’s velocity. Create a line of code that adds a point at a time t with a value of dot(block.velocity, unitPar).
If you do all of this correctly, running the main procedure should give a graph like the one shown below.
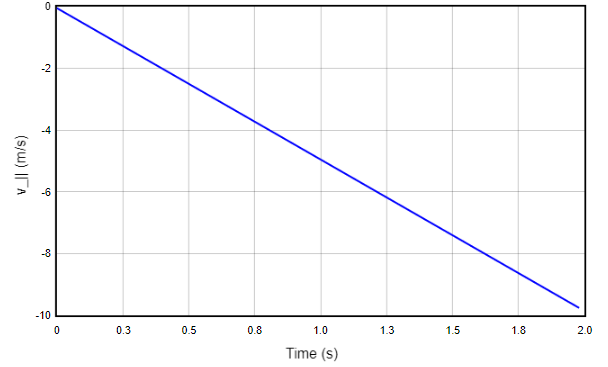
Fig. 14.9 Parallel velocity component with \(v_{i, ||} = 0\)¶
Because the acceleration has a constant magnitude of \(g \sin \theta\), the slope of the velocity vs. time graph is constant; it is also negative, since the acceleration is down the ramp.
Try different values of \(\theta\) (i.e. change the variable Q), and see how your velocity graph changes. If the angle increases, what happens to the value of the acceleration? Are the results what you expected?
Problem
A block slides down with the velocity along the smooth incline shown in the graph below. Find the angle (in degrees) of the ramp.
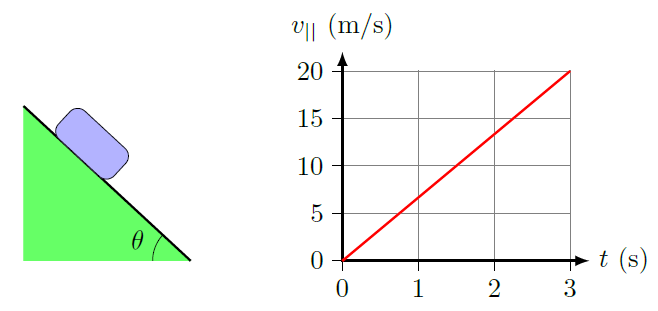
Fig. 14.10 Block on a smooth ramp, with a graph of its parallel velocity component \(v_{||}\)¶
Answer: \(42.8^\circ\)
Problem
What would a graph of the block’s position \(r_{||} = {\vec r} \cdot {\hat e}_{||}\) along the ramp vs. time look like? Is the slope of this line constant or changing? What does the slope of this position vs. time graph represent? Try adding the code needed to make this graph, and see if the graph matches your expectations.
Answer: You should get a curved graph, with a slope increasing in size. This is because the block is accelerating, so it has a greater speed; the size of the slope of a \(r_{||}\) vs. \(t\) graph would represent this speed.
Problem
What kind of motion do you get if the angle \(\theta = 0^\circ\)? If \(\theta = 90.0^\circ\)?
Answer: If the angle is \(\theta = 0^\circ\), there should be no acceleration at all, since the ramp is flat, and the block remains stationary. If the angle is \(\theta = 90.0^\circ\), the ramp is vertical, and the block should be in free fall. The acceleration would then have a magnitude of 9.81 m/s\(^2\).
The next step will be to give the block an initial velocity. Since the block cannot go into the ramp, or fly off the ramp, this initial velocity cannot be along the \({\hat e}_\perp\) unit vector. You will start with a velocity \({\vec v}_i = v_i {\hat e}_{||}\). To create this define a variable VEL_PAR_INIT in the “Constants and definitions” section of the code; set this variable to 5. You will also have to change block.velocity inside the definition of block. Remember that the block’s initial velocity has to have a magnitude of VEL_PAR_INIT and a direction parallel to the ramp. You will need only one of the unit vectors you defined to give this direction. Put this into your code now, and run the code. If you do this properly, you should get a graph like the one below.
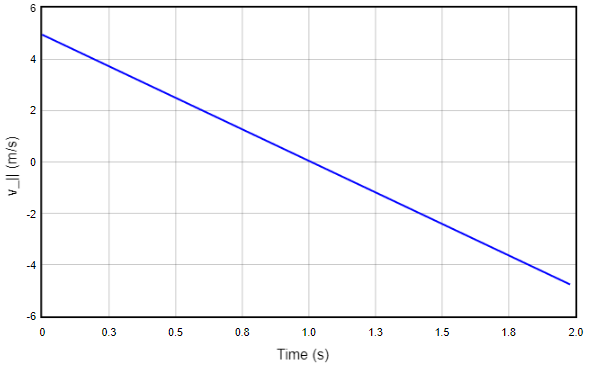
Fig. 14.11 Parallel velocity component with \(v_{i, ||} \ne 0\)¶
In this case, the block starts with a velocity up the ramp. However, the acceleration of the ramp still points down the ramp, so the block comes to a stop, and then starts moving down the ramp. Thus, the parallel velocity component starts positive, but becomes negative with a constant negative slope.
Problem
How does your velocity vs. time graph change if you alter VEL_PAR_INIT? If you change the angle variable Q with the same value of VEL_PAR_INIT?
Answer: Changing the initial speed would only change the starting position on the graph of the \(v_{||}\) component (i.e. the “y intercept”). Changing the angle gives a different acceleration magnitude for the block, and therefore a different slope of the \(v_{||}\) vs. \(t\) graph.
Problem
What would the block’s position \(r_{||}\) along the ramp vs. time \(t\) graph look like now that the block has an initial velocity? Would you expect anything to change with the position graph from when the initial velocity was zero? Again, try adding the code needed to create this graph, and see if it looks like what you guessed.
Answer: Because the initial velocity component along the ramp is not zero, the initial slope of the \(r_{||}\) vs. \(t\) graph would be different. However, the graph should still be curved, since the block is accelerating, and thus has a changing parallel velocity component.
Problem
Suppose a block is initially moving at a speed \(v\) up a ramp with an angle \(0.00^\circ < \theta < 45.0^\circ\); it moves a total distance of \(L\) before it momentarily comes to a stop. If the angle were doubled, so the block moves up a ramp with angle \(2 \theta\), but the starting speed was the same, how far would the block travel before coming to a momentary stop? Choose the best answer below.
The same distance \(L\)
More than half the original distance, but less than \(L\)
Half the original distance
Less than half the original distance
It depends on the angle \(\theta\)
Answer: Suppose the initial speed is denoted \(v\); then the distance traveled by the block before it stops will be
If we use the angle \(\theta_{new} = 2 \theta\), then
Thus, the ratio of the two distances is
Evaluated at the boundary angles, the ratio runs from 0.500 to 0.707, so the new distance is more than half the original distance, but less than the original.
14.7. Adding side-to-side motion¶
So far, we have used two directions relative to the ramp – perpendicular to the surface, and parallel to the ramp up and down the ramp. However, the block could potentially move in a third direction, parallel to the surface, but side-to-side rather than up and down the ramp. You will now create this type of motion with the block.
First, a third unit vector \({\hat e}_{side}\) must be defined to give the direction of this motion. It must be perpendicular to both \({\hat e}_{||}\) and \({\hat e}_\perp\). In other words,
If you think about it, there is a relatively simple choice for a vector that is (1) perpendicular to the other two unit vectors for all choices of the angle \(\theta\), and (2) has a magnitude of 1. If you have trouble seeing this vector, use the two equations above to create algebraic equations for the components \(A_s, B_s\), and \(C_s\) of the vector \({\hat e}_{side} = A_s {\hat x} + B_s {\hat y} + C_s {\hat z}\). Which component does not appear in these equations? You can freely choose this component to be whatever you want, but remember that you must also have
From this choice of vector, below unitPar and unitPerp, in your code for init(), define a third unit vector unitSide with the proper components. Then define a variable VEL_SIDE_INIT to represent the initial velocity component in the sideways direction, and give it a value of 1. Increase MAX_TIME so that it is now 3.
It may also be helpful to add a trail to the block, so you can see the path it takes. This can be done by adding make_trail = True to the definition of block. Now run the main procedure, and see how the change in initial velocity changes the motion. You should see the block move in parabolic path – it is still accelerating down the ramp, but the motion side-to-side is at a constant rate. This is much like projectile motion, with a smaller value of the acceleration (because of the ramp’s angle).
To see this in more detail, in the “Create velocity graph” part of the main procedure, add a new line to create velSideCurve. Use this to graph the component \(v_{side} = {\vec v} \cdot {\hat e}_{side}\) in a different color than you chose for velParCurve. Update velSideCurve in a manner similar to what you did for velParCurve, but make sure you change the dot product inside the code. If you did everything correctly, you should see the following graph.

Fig. 14.12 Parallel and sideways velocity components of block on inclined plane¶
Try creating corresponding graphs for the two components \(r_{||}\) and \(r_{side} = {\vec r} \cdot {\hat e}_{side}\) for the position of the block vs time. These should be similiar to the horizontal and vertical position vs. time graphs for a projectile.
14.8. Inclined planes with friction¶
Let’s now add friction to an object on an inclined plane or ramp. Because friction is involved, this means our first step is usually going to be solving for the normal force acting on the object. Then we use this to find the force of friction. Thus, it will be important to completely solve the Newton’s second law equations for the object on the ramp – meaning in both the parallel and perpendicular directions. We have already seen all the physics concepts we will use, so let’s go through an example, and see how all of the pieces fit together.
Suppose that a child slides down a playground slide with an acceleration magnitude of 1.26 m/s\(^2\). Assuming the slide is at a constant 33.0\(^\circ\) angle to the horizontal, what is the coefficient of kinetic friction between the slide and the child? As always, we first set up the FBD for the situation. The relevant forces here are the gravitational, friction, and normal forces. Since the acceleration is along the ramp, it makes sense to use unit vectors parallel and perpendicular to the ramp. The frictional force opposes the motion down the slide, so it points up the slide. Thus, the FBD looks like the diagram shown below.
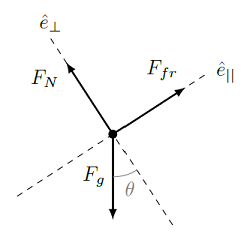
Fig. 14.13 FBD for child on slide¶
We start from the vector sum of the forces,
where
Note that up the ramp is taken as positive here. This means that the acceleration in this case is
where \(a = 1.26\) m/s\(^2\) is the magnitude of the acceleration. As always, watching your signs means thinking about the directions for each of the vectors involved in the problem! You will see below that if you had not included this sign for the acceleration, you would have gotten the wrong answer for \(\mu_k\). Taking the scalar product with the two unit vectors \({\hat e}_{||}\) and \({\hat e}_\perp\), we get
Before friction was involved, we could solve the \({\hat e}_{||}\) equation without really worrying about the \({\hat e}_\perp\) equation at all. Now that we have friction, we need to solve the \({\hat e}_\perp\) equation first for the magnitude \(F_N\) of the normal force, then substitute that into the \({\hat e}_{||}\) equation. So, going through this plan, we get
and so
Notice why we weren’t told the mass of the child – it cancels out of the equation! This is because \(m\) is in all the terms of the equation, so we can factor it out. Here’s another way to say it. If we double the mass of the child, for example, then the normal force and the child’s weight both double as well. These doublings cancel out in the Newton’s 2nd law equation, giving the same acceleration magnitude. Taking the \({\hat e}_{||}\) equation, and solving for the coefficient of kinetic friction \(\mu_k\) gives
With the numbers given above, this results in \(\mu_k = 0.496\).
Problem
A box sits on a flat board. You lift one end of the board, making an angle with the floor. As you increase the angle, the box will eventually begin to slide down. Why? Choose the best answer below.
The coefficient of static friction decreased
The component of gravity force parallel to board increased
The normal force exerted by board decreased
Both 1 and 2
1, 2, and 3 are all true.
Answer: The coefficient of static friction only depends on the two surface moved relative to each other, so this does not change. As the angle increases, the component \(F_{g, ||}\) of the gravitational force along the ramp will increase in size, while the normal force will decrease in size. It might help to think of the extreme case, when the board is straight up. Then, all of the force of gravity points along the board, while the normal force is essentially zero.
Problem
A mass \(m\) is placed on a rough inclined plane and slides down the plane with constant speed \(v\). If a block of mass \(2m\) were placed on the same incline, which choice describes what would happen in that case? Select the best choice.
The mass does not move at all.
The mass would slide a bit, slow down, then stop.
The mass would accelerate down the incline.
The mass would slide down at constant speed.
The mass would slide up at constant speed.
Answer: In the worked-out example above, the mass canceled out of the equation. This is because all the forces involved increase in exactly the same proportion as the mass itself (by doubling), so there is no effect from the change. This means the \(2m\) mass would slide down the ramp at constant speed, the same as the original \(m\) mass.
Problem
A horizontal force of 60.0 N is applied to a box of mass 6.40 kg which slides down an incline (\(\theta =20.0^\circ\)), as shown. The coefficient of kinetic friction between the box and incline is 0.240.

Fig. 14.14 A box on a ramp, with an applied force¶
What is the magnitude of the normal force (in N) on the box?
What is the magnitude of the acceleration (n m/s\(^2\)) of the box?
Answers: 38.5 N; 10.7 m/s\(^2\)
As another example, let’s see how we can experimentally determine the coefficient of static friction \(\mu_s\) for a substance with a simple measurement. Suppose we have a block sitting at rest on a ramp, and it stays at rest, because the force of static friction is enough to keep it in place. This means that static friction has a magnitude less than or equal to its maximum value:
The force equations for this block will be almost the same as in the last section. We don’t set \(F_{fr}\) equal to \(\mu_s F_N\) just yet, however. Thus, we have the force equation in the parallel direction is
since the block is not moving. From the inequality above, this means
We now take the left and right pieces of this inequality, and solve for the coefficient \(\mu_s\), resulting in
Thus, the coefficient of static friction \(\mu_s\) determines a maximum angle \(\theta_s = \tan^{-1} \mu_s\) known as the angle of repose. If the angle of the ramp is greater than this angle \(\theta_s\), then static friction is not enough to keep the block in place, and it will slide down the ramp. On the other hand, if the incline angle is less than \(\theta_s\), then a block started at rest will remain at rest on the ramp.
A consequence of this is that piles of a given material will always have a slope less than a particular value. If you watch the video linked below, you will see sand poured onto an existing sand pile. The angle of the pile with respect to the horizontal will never get to be more than about 35 degrees or so. If this does happen, the sand at the top will slide down, until the angle is again below the angle of repose. So, you can see that the coefficient of static friction for sand on sand is about \(\tan 35^\circ\), or around 0.700.
14.9. Summary¶
This lesson introduced the ideas involved for objects moving on a ramp or inclined plane. As you saw in the lesson overview section, this problem has a long history in physics! It is also a nice way to show the interrelationship between the gravitational and normal forces – the size of the normal force, compared to the object’s weight, can be easily changed by altering the ramp angle. The normal force will have a different magnitude for any given angle choice, showing how this force can vary, depending on what is necessary to keep the object from going through the ramp.
We also brought together the ideas of inclined planes and friction (from Lesson 12). This should give you some practice in applying Newton’s second law to a situation with multiple forces acting on an object. In particular, with an applied force included, this force can have components both parallel and perpendicular to the ramp. If the applied force has a perpendicular part, the normal force can change, thus altering the frictional force parallel to the ramp. Therefore, this is a situation where what is happening in one direction can affect the motion in a perpendicular direction. This will be the generic situation for force problems.
After this lesson, you should be able to:
Describe the normal force acting on an object.
Write down the Newton’s 2nd law equations for an object moving on an inclined plane.