.ipynb .pdf

Binder

Contents

7. Vector magnitude and direction

7.1. Overview

Links to programs in this lesson:

1. 3D vector components

2. Vector magnitude and direction

Over the past few lessons, you have seen how vectors are important when studying the motion of an object. The fundamental properties of motion – position, velocity, and acceleration – are all vectors. Thus, both their definitions, and the mathematical relationships between them, are vector equations. Even with the scalar kinematic equations, the vectors components of these quantities are used.

However, up to this point, we have only worked with components of vectors. For eample, in the last lesson, free fall only dealt with motion along the \(y\) axis. Suppose instead you are given the size and direction of a vector? An example would be saying the speed of a ship is 15.0 knots, and it is moving 30.0\(^\circ\) north of west. How can we write this in terms of components? Or, if we go the other way around, if I know the components of an acceleration, how can I find the magnitude and direction of this vector?

This is the purpose of this lesson – to learn how to go back and forth between writing a vector in terms of components, and using magnitude and direction to describe the vector. This will use the mathematics of trigonometry heavily, so it is important you get a good grasp on how this process works. After this lesson, you should have all the basic relations needed to go from one description of a vector to another. Along the way, you will learn more about unit vectors. In particular, you will see how to find a unit vector pointing in the same direction as any given vector. Once we have this down, we can move on to projectile motion in Lesson 08.

One important thing to remember is the components of a vector are the sizes of the vector along perpendicular directions (recall the streets and avenues of Manhattan in Lesson 02). This is why we use right triangle trigonometry, because the components are always going to be perpendicular. (You can be brave and use the law of cosines or sines if you know them, but you will quickly get bogged down by the time you try to add three vectors!)

Here are the objectives for this lesson:

• Given the magnitude and direction of a 2D vector, find its \(x\) and \(y\) components.

• Given the components of a 2D vector, find its magnitude and direction.

• Find the magnitude of a 3D vector.

• Given a vector, find the unit vector in the same direction.

7.2. Vector magnitudes

You are probably familiar with the Pythagorean theorem for right triangles, as shown below.

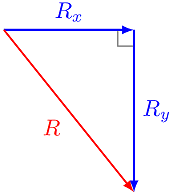
Fig. 7.1 The Pythagorean theorem for a right triangle formed by a vector \({\vec R}\)

\[ R^2 = R_x ^2 + R_y ^2 \Rightarrow R = \sqrt{R_x ^2 + R_y ^2} \]

If we have a two-dimensional vector (i.e. one with only two non-zero components), then we can use this version to find the magnitude (or size) of the vector, since the two legs are perpendicular to each other. How do we extend this to vectors with three non-zero components?

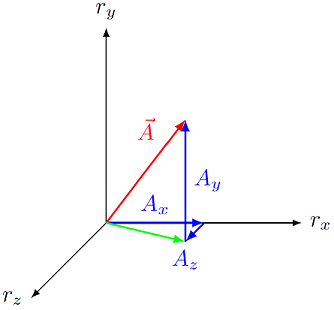
Fig. 7.2 The Pythagorean theorem for a three-dimensional vector

If you want a three-dimensional version of this picture, which you can move around, run the following program to see the same thing in vPython. I have added labels for each of the individual vector pieces, as well as the total (or resultant) vector \({\vec A}\). You can see the code by clicking on the pencil icon at the top left of the app.

Coordinate axes in vPython

The coordinate axes are different in vPython – the \(+z\) direction points out of the screen by default, while the \(+y\) direction points upwards – so the picture and the vPython view are not exactly the same! However, it does give you an idea of what the two-dimensional illustration above is trying to convey.

Back to program list

Back to Figure 7.2 above, let’s figure out how to find the magnitude of a three-dimensional vecor. First, we find the magnitude of the vector \({\vec R} = A_x {\hat x} + A_z {\hat z}\) in the \(x-z\) plane, using the 2D Pythagorean theorem (this is the length of the green arrow in the figure). This gives the relation

\[ R = \sqrt{A_x ^2 + A_z ^2} \]

This new vector now forms one of the legs of the full vector \({\vec A}\), made of all three components. Using the 2D Pythagorean theorem again for this new triangle gives the magnitude of the vector \({\vec A}\).

\[ A = \sqrt{R^2 + A_y ^2} \]

Finally, substituting in the length \(R\) from before gives the final answer in terms of the three components \(A_x, A_y\), and \(A_z\).

\[ A = \sqrt{A_x ^2 + A_y ^2 + A_z ^ 2} \]

So, the 3D Pythagorean theorem is built up from using the 2D version twice; if you feel motivated, you can keep going into higher dimensions!

Problem

Find the magnitude of the following vectors, with the appropriate units.

1. \({\vec C} = (15.0 \ \textrm{m/s}) {\hat x} + (7.66 \ \textrm{m/s}) {\hat z}\)

2. \({\vec D} = (-4.09 \ \textrm{km}) {\hat x} + (8.32 \ \textrm{km}) {\hat z}\)

3. \({\vec E} = (11.0 \ \textrm{N}) {\hat x} + (8.75 \ \textrm{N}) {\hat y} + (-17.2 \ \textrm{N}) {\hat z}\)

4. \({\vec F} = (20.6 \ \textrm{kg m/s}) {\hat x} + (-13.2 \ \textrm{kg m/s}) {\hat y} + (-18.4 \ \textrm{kg m/s}) {\hat z}\)

Answers: \(C = 16.8\) m/s; \(D = 9.27\) km; \(E = 22.2\) N; \(F = 30.6\) kg m/s

7.3. Unit vectors

When we introduced vectors and vector components, we saw how any vector can be divided up into three pieces – the vectors describing how much of the vector is along each of the three coordinate axes \(x, y\), and \(z\). For example, any vector \({\vec A}\) can be written as

\[ {\vec A} = A_x {\hat x} + A_y {\hat y} + A_z {\hat z} \]

Here, \(A_x, A_y\), and \(A_z\) are the components of the vector, while \({\hat x}, {\hat y}\), and \({\hat z}\) are the three unit vectors. Recall that a unit vector has unit size (i.e. length of one); the unit vector \({\hat x}\) has length of one and points in the \(+x\) direction. So, if we were to define these as vectors in vPython, then the three unit vectors xUnit, yUnit, and zUnit would be

xUnit = vector(1, 0, 0)
yUnit = vector(0, 1, 0)
zUnit = vector(0, 0, 1)

This way of writing \({\vec A}\) as the sum of three vectors, one along each coordinate axis, is shown below.

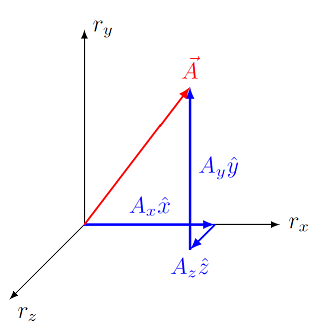
Fig. 7.3 Decomposition of a vector \({\vec A}\) using unit vectors \({\hat x}, {\hat y},\) and \({\hat z}\)

However, there is no reason to have unit vectors only along the coordinate axes. In fact, we can find a unit vector that points in the same direction as any vector. This has various applications, but most of them boil down to the need to separate the magnitude of a vector from its direction; the unit vector encodes the direction, and it is multiplied by a scalar to give the magnitude. You will see pop up in such disparate places as the universal force of gravitation, and electric fields.

To do this, we can take an arbitrary vector \({\vec A}\), and divide it by its magnitude \(A\). Since this is just scalar multiplication of a vector, this gives a new vector; because we are dividing the vector by its magnitude, the new vector will have length of one. This gives us the definition of a unit vector \({\hat A}\) as the vector pointing in the same direction as an arbitrary vector \({\vec A}\), but with a magnitude of 1. In math terms, this means

\[ {\hat A} = \frac{{\vec A}}{A} \]

Problem

For the vector \({\vec A} = 12 {\hat x} - 20 {\hat y} + 9 {\hat z}\), find the unit vector \({\hat A}\) pointing in the same direction as \({\vec A}\).

Answer: \({\hat A} = 0.480 {\hat x} - 0.800 {\hat y} + 0.360 {\hat z}\)

Remember not to confuse the different quantities, which are denoted by the symbol going along with it (or lack of one!): \({\vec A}\) is a vector, \(A\) (no symbol on top) is the magnitude of \({\vec A}\), and \({\hat A}\) is a unit vector pointing in the same direction as the vector \({\vec A}\). The figure below shows both \({\vec A}\) and \({\hat A}\); both vectors start at the marked point.

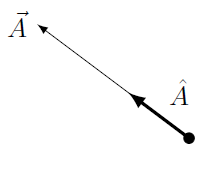
Fig. 7.4 Defining a unit vector \({\hat A}\) from a given vector \({\vec A}\)

Conveniently for us, vPython has commands that find both the magnitude of a vector, and find the unit vector in the same direction as another vector. The first is done with the mag module, the second uses the norm module. If we define the vector \({\vec A}\) by using the command

A = vector(12, -20, 9)

then we can find the magnitude of this vector in vPython by using the command

mag(A)

In addition, we could get a unit vector by using the defining equation

\[ {\hat A} = \frac{{\vec A}}{A} \]

This is done using another vPython command,

norm(A)

which directly takes a vector and finds the unit vector. Try this in a vPython program, using Trinket or Glowscript. Using either method, you should get the vector <0.48, -0.8, 0.36>, which in unit vector notation would be \((0.48) {\hat x} + (-0.8) {\hat y} + (0.36) {\hat z}\). So we now have the new vPython commands

• mag(A): Find the magnitude of a vector A

• norm(A): Find a unit vector in the same direction as vector A

The command hat(A) will also find the unit vector in the same direction as the vector A.

7.4. Finding vector components

Hopefully, you have seen the trigonometric functions before sometime in your academic career. Here is a quick summary to remind you of their properties.

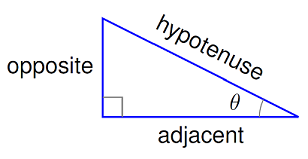
Fig. 7.5 Right triangle with sides labeled based on the location of the angle \(\theta\)

• The (S)ine function of an angle \(\theta\) is found by the ratio of the side (O)pposite the angle over the (H)ypotenuse, or SOH:

\[ \sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} \]

• The (C)osine function of the angle is given by the ratio of the (A)djacent side over the (H)ypotenuse, or CAH:

\[ \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} \]

• The (T)angent function of \(\theta\) is given by the ratio of the (O)pposite side to the (A)djacent side, or TOA:

\[ \tan \theta = \frac{\text{opposite}}{\text{adjacent}} \]

You may have heard of the mnemonic “SOHCAHTOA” to keep track of which trig function goes with which sides of the triangle. Remember, though, that the sides are relative to the position of the angle – if you look at the other angle in the triangle, that switches which side is the opposite, and which is the adjacent.

The application below looks at the relationship between the angle, the trigonometric functions, and the unit circle. It is a good review if you are feeling shaky on these equations; you need to get good at them!

As long as you know one angle (other than the right angle) and one side, you should be able to find the other two sides. The next problem gives you practice in using the trig functions to solve for an unknown side of a right triangle, using another side and an angle.

Problem

For each of the following, find \(x\) to three sig figs.

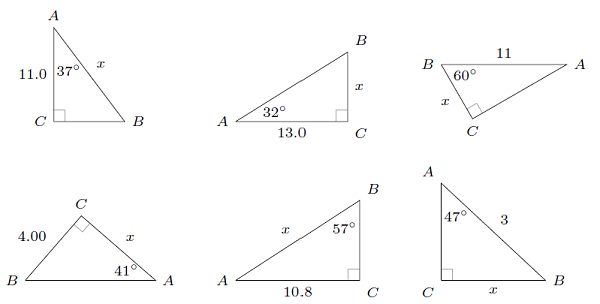
Fig. 7.6 Finding the length of the missing side \(x\), based on the given side and angle

Answers: The answers are shown for each triangle in the graphic below.

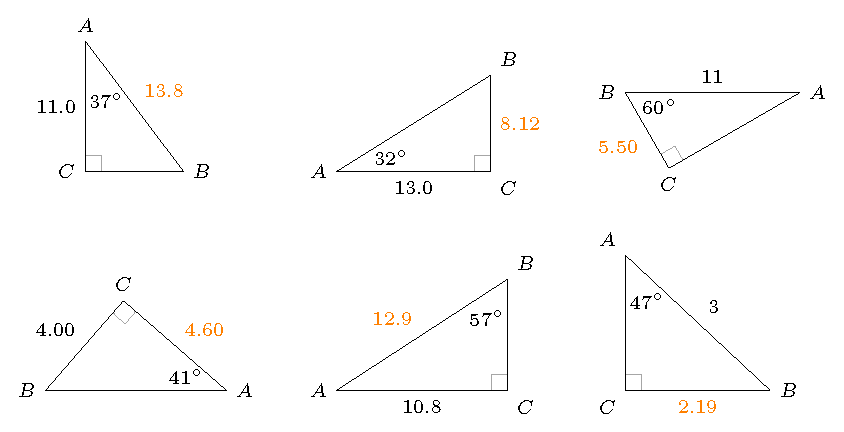
Fig. 7.7 The missing sides \(x\), based on the given side and angle

Now we have the mathematical framework to find the components of a vector, if we know the magnitude and direction of the vector. In other words, if we form a right triangle, with the hypotenuse given by the magnitude, and one of the angles coming from the vector direction, the \(x\) and \(y\) components of the vector will be the two sides of the right triangle. Before we go through that, though, we should talk about how directions are specified for vectors. There are a few ways you might see this. The first is to give an angle \(\theta\) between \(0^\circ\) and \(360^\circ\), and say the vector points at “\(\theta\) degrees counterclockwise (or CCW) from the \(+x\) axis”. This is often how you see angles given in math class, for example. However, you need to use this to create a right triangle, so you need to find an angle between \(0^\circ\) and \(90^\circ\). This is where drawing a vector diagram is helpful, to figure out this angle. The process is shown in the figure below, for a vector pointing \(240.^\circ\) CCW from the \(+x\) axis. Since the \(-y\) axis is 270.\(^\circ\), and “too far CCW around the circle”, we have to subtract \(270.^\circ - 240.^\circ\) to get the remaining angle \(\theta\). This gives the angle of \(\theta = 30.0^\circ\) in the vector diagram on the right hand side.

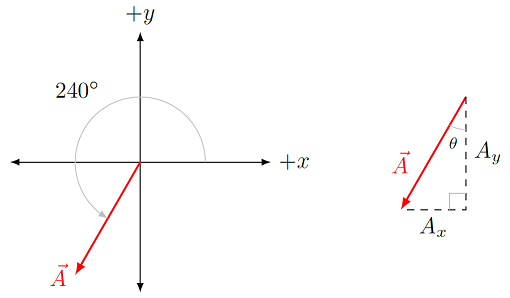
Fig. 7.8 Going from the math notation for an angle to the vector diagram

Another way to give the direction of a vector is in terms of the cardinal directions: north, south, east and west (NSEW). Here, one would say something like “\(30.0^\circ\) west of south”. Notice the way this is given – as a turn from the start. You start pointing south, then turn \(30.0^\circ\) westward. This gives exactly the same vector diagram before, it is just phrased in a difference way. You should be careful, though – \(30.0^\circ\) west of south is not the same thing as \(30.0^\circ\) south of west!

Give the right directions

Whenever you work through a problem, and need to report the direction of a vector, you answer should match the format the problem is given in. If you have vectors in NSEW format, then your vector direction should be written in the same way. But if you are only given an angle CCW from the \(+x\) axis, your resulting vector should be reported in math notation as well. Don’t switch formats!

Problem

Which description below gives the best correct direction for the red vector shown in the picture below?

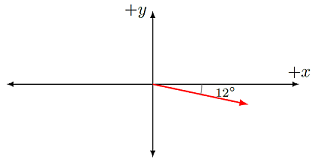
Fig. 7.9 Example of a vector direction

1. \(12.0^\circ\) counterclockwise from the \(+x\) axis

2. \(12.0^\circ\) east of south

3. \(78.0^\circ\) east of south

4. \(78.0^\circ\) south of east

5. \(348^\circ\) counterclockwise from the \(+x\) axis

Answer: The vector is defined using the \(x\) and \(y\) coordinate axes; there are no NSEW directions involved, so these should not be used. Using the usual math convention, this vector would be described as “\(348^\circ\) counterclockwise from the \(+x\) axis”.

Now let’s get into how to go from magnitude and direction to vector components. Suppose we are given that a person’s velocity \({\vec v}\) is 8.00 m/s at 40.0\(^\circ\) south of west, and we want to express this 2D vector in vector components. Any 2D vector can be drawn in terms of a right triangle, where the hypotenuse is the magnitude of the vector, and the two sides are the \(x\) and \(y\) compnents of the vector.

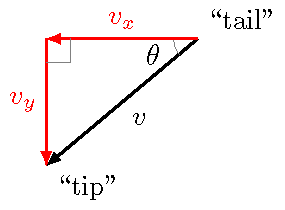
Fig. 7.10 Using right angle trigonometry to find vector components

Here are the individual steps I used when going through the work in the figure above, starting from the velocity vector given. Draw a diagram of the vector pointing in its actual direction. From the starting point (the “tail”), ask yourself “which way do I need to move horizontally to go from tail to tip?” Then ask “Which way do I need to move vertically to get to the tip?” Notice in these last two steps, we are using our graphical vector addition skill to draw the vector. Make sure you construct a proper right triangle! This is my vector diagram: a drawing of a vector, and its vector components, using graphical vector addition, along with the correct labels for each of the three arrows and the appropriate angle. You should get into the habit of always drawing such a diagram, to avoid making silly mistakes! Apply your right triangle mathematics (SOHCAHTOA) to determine the \(x\) and \(y\) components of the vector (including signs!). This gives an answer of \(v_x = - v \cos \theta = -6.13\) m/s and \(v_y = -v \sin \theta = -5.14\) m/s. Both are negative, since the vector \({\vec v}\) lies in the third quadrant.

Problem

Which of the following components correctly describe a velocity of 10.5 m/s, 105\(^\circ\) CCW from the positive \(x\) axis?

1. \(v_x = -2.72\) m/s, \(v_y = -10.1\) m/s

2. \(v_x = -2.72\) m/s, \(v_y = +10.1\) m/s

3. \(v_x = -1.72\) m/s, \(v_y = +10.4\) m/s

4. \(v_x = +2.72\) m/s, \(v_y = -10.1\) m/s

5. \(v_x = +2.72\) m/s, \(v_y = +10.1\) m/s

Answer: Since the angle is 105\(^\circ\) CCW from the positive \(x\) axis, the vector is in the second quadrant, so \(v_x < 0, v_y > 0\). This eliminates all but two choices. Drawing the correct triangle gives that \(v_x = -2.72\) m/s, \(v_y = +10.1\) m/s.

Problem

Find the unit vector notation for the following vectors, with the appropriate units.

1. 7.26 m at 37.4\(^\circ\) CCW from \(+x\) axis

2. 14.1 m/s at 208\(^\circ\) CCW from \(+x\) axis

3. 8.09 N at 335\(^\circ\) CCW from \(+x\) axis

4. 4.83 kg m/s at 27.5\(^\circ\) north of west

5. 2.46 km at 75.3\(^\circ\) east of south

Answers:

1. \((5.77 \ \textrm{m}) {\hat x} + (4.41 \ \textrm{m}) {\hat y}\)

2. \((-12.4 \ \textrm{m/s}) {\hat x} + (-6.62 \ \textrm{m/s}) {\hat y}\)

3. \((7.33 \ \textrm{N}) {\hat x} + (-3.42 \ \textrm{N}) {\hat y}\)

4. \((-4.28 \ \textrm{kg m/s}) {\hat x} + (2.23 \ \textrm{kg m/s}) {\hat y}\)

5. \((2.38 \ \textrm{km}) {\hat x} + (-0.624 \ \textrm{km}) {\hat y}\)

Problem

Write a vPython function calcComps() that calculates the \(x\) and \(y\) components of a vector, given its magnitude and direction. The arguments of this function are the magnitude V and direction angle Q (in degrees CCW from the \(+x\) axis) of a two-dimensional vector \({\vec v}\); you can assume that \(v_z = 0\). The function will return a list [Vx, Vy] of the two non-zero components Vx and Vy of the vector. Remember that the vPython functions sin() and cos() take angles in radians, not degrees!

If you have never seen these before, it is an alternate (and probably more sensible!) angular unit, with one complete turn around the circumference defined as \(2 \pi\) radians. This means the conversion factor between degrees and radians is

\[ 1 \textrm{ radian} = \bigg( \frac{180}{\pi} \biggr) \textrm{ degrees} \]

We can get vPython to do the conversion for us – if Q is the angle in degrees, radians(Q) will be the corresponding radians measurement. If you go back to the ‘Trig Tour’ application given previously in this lesson, you can change the angle measurement back and forth between degrees and radians, and see what the relationship is for the unit circle, and all of the trig functions.

Answer: Here is a possible solution.

def calcComps(V, Q):

    # Convert angle from degrees to radians
    
    Q = radians(Q)
    
    # Find components; notice that the
    # functions sin, cos will give the
    # correct sign as well, so no need to
    # check further
    
    Vx = V * cos(Q)
    Vy = V * sin(Q)
    
    # Return results as list
    
    return [Vx, Vy]
    

7.5. The inverse trigonometric functions

The inverse trigonometric functions are often confusing to students. Part of the reason is that the notation does not mean what you may think it means! Often, this is because you are used to only using multiplication and division, addition and subtraction. So let’s start with these operations, and then talk about “taking the inverse”.

When I want to “undo” multiplication, I can use the division operation. For example, if I have \(ab = c\), and I want to solve for \(a\), then I divide by \(b\):

\[ ab = c \Rightarrow \frac{(ab)}{b} = \frac{c}{b} \Rightarrow a = \frac{c}{b} \]

In the original equation, \(a\) was multiplied by \(b\), so to undo this, and get \(a\) by itself, I had to divide by \(b\). This is what “inverse” means to a mathematician – what operation “undoes” another? Whenever you see the \(( )^{-1}\), this means we are taking the inverse of whatever is inside the parentheses. Said another way, if I do a mathematical operation, and then perform its inverse, I should get back to where I started!

So, now we have the trigonometric functions, which take an angle \(\theta\) and give you a ratio (which one depends on which function!). Taking the inverse would reverse the process: start with a ratio, and give the angle \(\theta\). So, for example, taking the inverse sine of the sine function should get me back to the angle:

\[ \sin^{-1} (\sin \theta) = \theta \]

Thus, the inverse trigonometric functions are great when you only know the sides of the triangle, and want to find the angle. Using the inverse sine on both sides of the original definition of sine, we get

\[ \sin \theta = \frac{O}{H} \Rightarrow \sin^{-1} (\sin \theta) = \sin^{-1} \biggl( \frac{O}{H} \biggr) \Rightarrow \theta = \sin^{-1} \biggl( \frac{O}{H} \biggr) \]

Inverse trig functions are not division

\(\sin^{-1} (O/H)\) is not the same thing as \(1/\sin (O/H)\)! The trigonometric functions are quite complicated functions when you write them out in terms of \(\theta\); their inverses are just as complicated. This is why we use the shorthand \(\sin^{-1}\), etc. for these functions. Taking the inverse sine of both sides of an equation is very different from dividing both sides by the sine function.

Going through the same process for the other two trig functions gives something similar. Therefore, the angle can be found by using any of the inverse trig functions. From the sine function, we get

\[ \theta = \sin^{-1} \biggl( \frac{\text{opposite}}{\text{hypotenuse}} \biggr) \]

while from the cosine function,

\[ \theta = \cos^{-1} \biggl( \frac{\text{adjacent}}{\text{hypotenuse}} \biggr) \]

and from the tangent function,

\[ \theta = \tan^{-1} \biggl( \frac{\text{opposite}}{\text{adjacent}} \biggr) \]

These functions are sometimes known as “arc sine”, “arc cosine”, and “arc tangent”.

Problem

For each triangle below, find \(\theta\) to three sig figs.

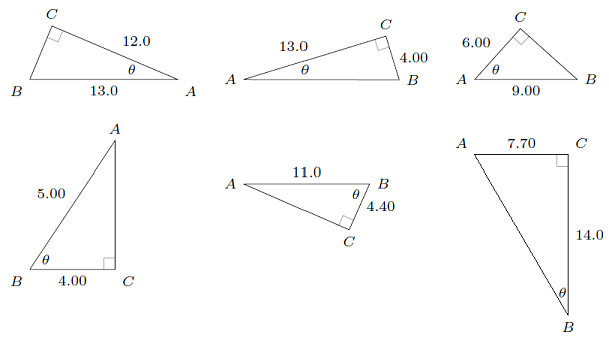
Fig. 7.11 Find the angle from the two given sides

Answers: The missing angles for each triangle are given in the graphic below.

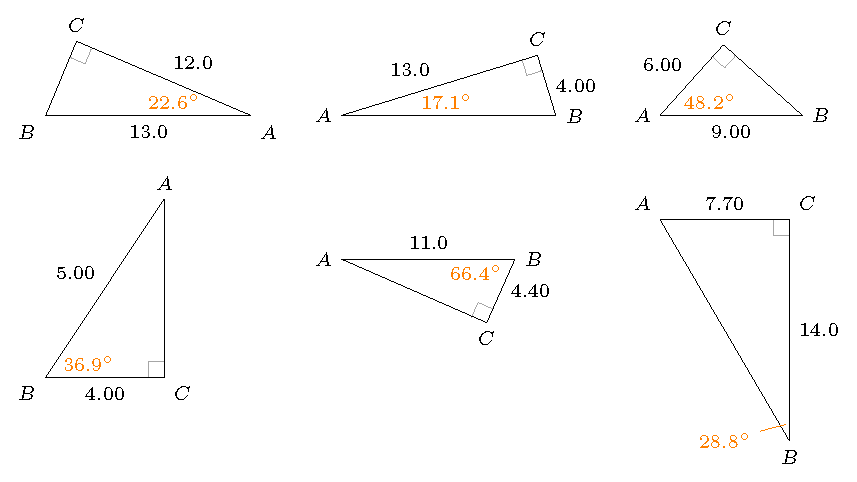
Fig. 7.12 The missing angles

7.6. From components to magnitude, direction

Let’s recap where we are. From the Pythagorean theorem (either 2D or 3D), I can find the magnitude of a vector if I know all of its components. Now, with the inverse trigonometric functions, if I know two sides of a right triangle, I can find either of the remaining two angles. This is enough to go from the vector component description of a vector, to get to its magnitude and direction. As an example, start with a vector given in components,

\[ a_x = +3.00\ \textrm{m/s}^2 \qquad a_y = +4.00\ \textrm{m/s}^2 \]

Below is the vector diagram for the vector \({\vec a}\).

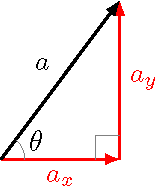
Fig. 7.13 Find the magnitude and direction of a vector from its components

I can now find the magnitude and direction, by using the process outlined above: Pythagoran theorem and inverse trig functions. Here are the specific steps I used to get the numbers in the figure above. Draw the \(x\) component; be sure to draw in direction matching its sign! At the end of the \(x\) component, draw the \(y\) component (“tip-to-tail” graphical vector addition). Again, the last two steps are to draw the relevant vector diagram. Where you originally started, begin a vector, then draw the vector to where you ended to create a right triangle. Use Pythagorean theorem for magnitude, and the inverse tangent for direction: 5.00 m/s\(^2\) at 53.1\(^\circ\) counter-clockwise from \(+x\) axis.

The triangle is a vector sum

Notice that I did not go back to the origin when drawing the final vector, based on its components! We are always drawing vectors “tip-to-tail”. This is a common mistake students make, and leads them to finding the wrong final angle. This diagram represents the sum of total vector as component vectors, using graphical vector addition.

Problem

Chris walks from the CVS to the library by first traveling two blocks west, then one block north. What is the magnitude and direction of the trip?

1. 2.24 blocks, 26.6\(^\circ\) north of west

2. 2.24 blocks, 26.6\(^\circ\) west of north

3. 3.00 blocks, 26.6\(^\circ\) north of west

4. 3.00 blocks, 26.6\(^\circ\) west of north

5. 5.00 blocks, northwest

Answer: The magnitude is 2.24 blocks, and the direction is 26.6\(^\circ\) north of west. Notice that, since the \(x\) (or westward) component is twice as large as the \(y\) (or northward) component, the vector is closer to the \(x\) axis.

7.7. Finding vector components in vPython

We saw earlier how to take a vector in vPython, and find its magnitude. Let’s now reverse the process, and start from a magnitude and direction, then find the corresponding vPython vector.

You will now create a vector bVec of a certain length and direction. The variable B will represent its magnitude, while Q will be its angle counter-clockwise from the \(+x\) axis; we will keep our vectors in the \(x-y\) plane, to stay simple. The program below includes two curves xAxis and yAxis, to show the \(x\) and \(y\) axes of the coordinate system. They also have labels xLabel and yLabel to show which one is which. Then, the magnitude B and direction Q (in degrees!) are defined, and a green arrow is created to show the vector \({\vec B}\).

Problem

Based on the choice of B and Q in the code below, what do you expect the arrow to look like? Which quadrant is it in? Run the program, and see if your guess is correct.

Back to program list

Change the values of B and Q_B, and see how it affects the size and direction of the arrow.

Problem

Add a second arrow cVec to the program above, to show a second vector \({\vec C}\). Define its magnitude C and direction Q_C in the appropriate place, and give the arrow a different color.

Answer: Your code should mirror what was done above for the vector \({\vec B}\); replace all the definitions for B and Q_B with similar definitions for C and Q_C. The code would look like the following, using the color yellow.

cVec = arrow(pos = vector(0, 0, 0), color = color.yellow, shaftwidth = 0.1, \
             axis = vector(C * cos(radians(Q_C)), C * sin(radians(Q_C)), 0))

Problem

Suppose you wanted to define a unit vector \({\hat B}\) pointing in the same direction as the vector \({\vec B}\). What would be the mathematical equation for the components of this vector? How would you program this into vPython?

Answer: One way to do this is to use the norm() command on the previously defined vPython vector B. However, an easier way to do this is note that the unit vector has a magnitude of 1, so we divide by B. This just gives the vector

bHat = arrow(pos = vector(0, 0, 0), color = color.green, shaftwidth = 0.1, \
             axis = vector(cos(radians(Q_B)), sin(radians(Q_B)), 0))

The magnitudes were removed from the definition of bHat.axis, since they cancel out when dividing by \(B\).

Challenge

Can you describe a three-dimensional vector in terms of a magnitude and direction? How many angles would you need to specify the direction? Remember, you can check the equations for your three vector components by using the 3D Pythagorean theorem, which should give you your original magnitude back. Hint: To check with the three-dimensional Pythagorean theorem, use the trigonometric identity \(\sin^2 \theta + \cos^2 \theta = 1\).

7.8. Summary

You have now learned everything you need to know about vectors. In Lesson 02 (introduction to vectors), you learned about graphical vector addition, vector components and unit vector notation, and how to add vectors using components. Now, in this lesson, you practiced finding the components from the magnitude and direction of a vector, and vice versa. You also saw the definition of a unit vector; we will periodically use this concept, starting with Lesson 07 (projectile motion). Since we will frequently use vectors in this class, you should use this lesson, and Lesson 02, as references whenever you need to refresh your memory about particular ideas.

After this lesson, you should be able to:

• Use the trigonometric functions to find the unknown side or angle in a triangle.

• Use the 3D Pythagorean theorem to find the magnitude of a given vector.

• Given the magnitude and direction of a vector, find its \(x\) and \(y\) components.

• Given the components of a vector, find its magnitude and direction.

• Given an arbitrary vector, find the unit vector pointing in the same direction.

6. Kinematic equations 8. Projectile motion