.ipynb .pdf

Binder

Contents

15. Fluids

15.1. Overview

Anything that you do in the sea services depends fundamentally on the properties of fluids. If you fly aircraft, you maintain altitude because of the lift on the wings or blades of your vehicle. The depth your submarine cruises at is a result of how much air versus water the boat has in its ballast tanks. Whether you are a sailor or a marine, your ship stays on the water because a naval architect has ensured the ship is buoyant and maintains its stability in choppy weather. Air and water are two prominent examples of fluids, but there are many others you can probably think of.

It is important to realize that “buoyant force” refers to the total force a fluid exerts on an object; however, this force results from the difference in pressure on the top and bottom of the object. The pressure on the bottom is almost always greater, giving an upwards buoyant force. Therefore, this lesson starts with the idea of pressure, and builds on that to develop the buoyant force. It was the great thinker Archimedes who came up with a relatively simple way to find the buoyant force, over two thousand years ago. If you use the resulting Archimedes’ principle, you will have an able guide to understand situations with fluids.

Here are the objectives for this lesson:

• Define pressure and density.

• State the density of fresh water.

• State the value of standard atmospheric pressure in SI units.

• Explain Pascal’s principle.

• Explain the relationship between pressure and depth in a fluid.

• Solve for the column height of a fluid in a U-tube using Pascal’s principle.

• State Archimedes’ Principle.

• Calculate the buoyant force on submerged or floating objects.

15.2. Fluids

15.2.1. Definition of a fluid

A fluid is a substance that can readily flow from place to place and take on the shape of a container. Fluid can be a liquid or a gas. For any type of object, fluid or otherwise, we can define the density of the object as its mass divided by its volume.

• Quantity: density

• Symbol: \(\rho\) (“rho”)

• Definition: For an solid object, or volume of fluid, with mass \(M\) and volume \(M\), the density is given by

\[ \rho = \frac{M}{V} \]

• Units: kg/m\(^3\)

You should memorize the density of fresh water as 1000 kg/m\(^3\).

Problem

A cube of metal has a mass of 347 g and measures 3.21 cm on a side. Using the table of densities given, identify the metal.

Substance	\(\rho\) (kg/m\(^3\))
aluminum	2700
iron	7860
silver	10500
lead	11300
mercury	13600
gold	19300

Answer: silver (Ag)

Historically, one of the more important ideas in physics from the 18th and 19th centuries is the kinetic theory of gases, which explains many of the properties of a gas by the simple model of assuming the gas is made of very small particles moving at random speeds. A good simulation to explore this model, and to review how it accounts for the various gas laws, is given below. You can also explore the distribution of kinetic energies for all of the particles in the gas, including the case where there are two different kinds of particle involved.

15.3. Pressure

15.3.1. Definition of pressure

Now that we have a simple model of a fluid, let’s use it to get an intuition for how fluids generate pressure. Consider what happens when you push both a pin and the blunt end of a pen against your skin with the same force. What will determine whether your skin will be punctured? Or how you “feel” this push? It turns out your skin actually measures the amount of force over a given area, not the absolute size of the force. So, if you exert the same force, but over a larger portion of your body, it does not feel as painful as if you apply the same force to a small area.

Thus, the ratio of force over area is important for determining how painful such prods are, among a lot of other things! The ratio is called the pressure.

• Quantity: pressure

• Symbol: \(P\)

• Definition: For a force \(F\) acting perpendicular to an area \(A\), the pressure is given by

\[ P = \frac{F}{A} \]

• SI units: pascals (Pa), with 1 Pa = 1 N/m\(^2\)

For example, squeezing an egg from all sides will not break the egg. The curved shape of the egg is able to redistribute the force all across its area, so the resulting pressure on the egg is too small to break the shell. However, exerting a force on a small area – by hitting the egg against the edge of a bowl – results in a large enough pressure to crack the egg!

Problem

You are walking out on a frozen lake and you begin to hear the ice cracking beneath you. What is your best strategy for getting off the ice safely? Choose the best answer.

1. Jump up and down to lessen your contact time with the ice.

2. Lie down flat on the ice and crawl toward shore.

3. Shuffle your feet (without lifting them) to move toward shore.

4. Stand absolutely still and wait for rescue.

Answer: You want to decrease the pressure you exert on the ice as much as possible. Since you cannot change your weight, you must increase your contact area with the ice, so you need to lie down flat, then crawl to shore.

Problem

A 60.0 kg woman is standing up such that the weight is distributed equally on both feet. If her heels are supporting 75.0 percent of her weight and the contact area between her heels and the ground are 0.250 in\(^2\) (for the high heel) and 2.00 in\(^2\) (for the flat heel), what is the pressure value on each heel?

Fig. 15.1 Two types of heel (high and flat) give different pressures on the foam beneath them

Answers: 1.37 MPa (high heel), 171 kPa (flat heel)

15.3.2. Atmospheric pressure

Although we do not notice it, the air around us exerts a pressure at all times. This is known as the atmospheric pressure, and is due to the weight of the air above. If you live at a high altitude, there is less air above you, so the atmospheric pressure decreases.

• Quantity: atmospheric pressure

• Symbol: \(P_{at}\)

• Definition: The standard atmospheric pressure at the surface of the Earth is 101.3 kPa. If a problem does not give the atmospheric pressure, you may assume a standard pressure of 101.3 kPa.

There are other non-SI units that you will see when dealing with pressure. One unit is the atmosphere (atm), which is the standard average pressure \(P_{at}\) at sea level on the Earth’s surface. Another such unit is pounds per square inch (psi), with 101.3 kPa (or 1 atm) the same as 14.7 psi; most tire gauges measure the pressure of vehicle tires in psi. You might also see units of mm of Hg (Torr). Torr are most often used when measuring blood pressure or by meteorologists discussing the weather!

Fig. 15.2 A tire gauge is used to measure the difference in the pressure inside the tire above atmospheric pressure

You can measure the atmospheric pressure by using a device called a barometer. A barometer is formed when a tube filled with fluid and blocked at both ends is put into a basin of the same fluid, and the bottom end is uncapped.

Fig. 15.3 A Goethe barometer, originally developed by the German writer Johann Wolfgang Von Goethe (source)

The fluid level in the top of the tube will go down to some level and stay. Why is this? Based on Aristotle’s ideas – “nature abhors a vacuum” – it was originally believed that a vacuum was formed and could pull the fluid up with a limited amount of force. However, this idea was tested by various people in the 1630s and 1640s. Evangelista Torricelli thought instead it was the weight of the air itself pushing the fluid up, until the forces from the air and fluid weights balanced.

Fig. 15.4 Portrait of Evangelista Torricelli (source)

This idea was tested by Blaise Pascal in various ways in 1644, with Pascal showing that Torricelli was correct. One way Pascal did this was to convince his brother-in-law to climb a local mountain with a barometer, and record the heights of the fluid in the barometer at various altitudes. His brother-in-law did this, accompanied by several of the local dignitaries, and they saw a clear decrease in the fluid height.

Fig. 15.5 Portrait of Blaise Pascal (source)

If we want to measure the pressure in our car or bicycle tires, we can use a pressure gauge. Note that the gauge does not measure the absolute pressure. It is much easier to measure the difference in pressure between that in the tire and the air outside. This is because this difference can be quickly measured by finding the net force on a given area. The force will be the difference in the forces from the atmospheric pressure, and from the pressure inside the tire. Thus, gauge pressure is the difference between total pressure and atmospheric pressure for a given situation.

• Quantity: gauge pressure

• Symbol: \(P_g\)

• Definition: When measuring the total pressure \(P_{tot}\) at a point in the atmosphere, the gauge pressure is the amount of pressure over the standard atmospheric pressure; thus,

\[ P_g = P_{tot} - P_{at} \]

Problem

A glass bottle of soda is sealed with a screw cap. The absolute pressure of the carbon dioxide inside the bottle is 160 kPa. Assuming the top and bottom surfaces of the cap each have an area of 4.74 cm\(^2\), obtain the magnitude of the force (in N) the screw thread exerts on the cap in order to keep it on the bottle. The air pressure outside the bottle is one atmosphere. Neglect the weight of the cap, which is very small compared to the forces due to the inside and outside pressures.

Answer: 28.0 N

Problem

The weight of your 1420 kg car (2019 Corvette ZR1) is supported equally by its four tires, each inflated to a gauge pressure of 35.0 psi. What is the area of contact each tire makes with the road (in cm\(^2\))?

Fig. 15.6 2019 Chevrolet Corvette ZR1 at the Montreal International Car Show (source)

Answer: 144 cm\(^2\)

15.4. Pressure at a depth

15.4.1. Pressure-depth relationship

If you measure the pressure at a particular point in a fluid, you are measuring the weight of all the fluid above that point acting on the area of your pressure gauge. Thus, for a denser fluid, the weight would be larger, even if nothing else changed, since there is more mass above the point. Similarly, if you take the container of fluid to another planet, with a different gravitational field, the weight will change for that reason. Finally, if you change the depth of the point you are measuring, there will be more or less fluid above that point, giving a different pressure reading. Notice that moving horizontally will not change the pressure, since the amount of fluid above the point has not changed.

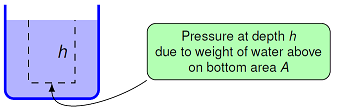
Fig. 15.7 Pressure at a depth in a fluid

We can work out this pressure \(P\) at a given depth \(h\) in the fluid by imagining we have an area \(A\) that we are measuring the pressure with – this may be the surface of our pressure gauge, for example. The weight of fluid above that area will be due to all the mass above it. To find this mass, we can think of it as forming a cylinder above the area \(A\), with a height the same as the depth \(h\). Thus, the volume of this cylinder is \(Ah\). We can write the mass \(m\) of the fluid in terms of the fluid density \(\rho_{fl}\) as

\[ m = \rho_{fl} V = \rho_{fl} A h \]

This means that there is a gravitational force on the pressure gauge area \(A\) given by the weight of the fluid above, or \(F_g = mg = \rho_{fl} g A h\). However, if we find the actual pressure on our gauge area \(A\), the area cancels out! This gives us that the change in pressure \(\Delta P\) due to a change in depth \(\Delta h\) in a fluid with density \(\rho_{fl}\) is

\[ \Delta P = \frac{F_g}{A} = \frac{\rho_{fl} g A \Delta h}{A} = \rho_{fl} g \Delta h \]

So, for example, imagine you are swimming in a pool. At a particular depth \(h\) of water, there is a pressure difference \(\Delta P\) between the pressure at the surface of the pool (assumed to be the standard atmospheric pressure \(P_{at}\)), and the total pressure \(P_{tot}\) at the depth \(h\). This means \(\Delta P = P_{tot} - P_{at}\), so we can find the total pressure at the depth \(h\) using

\[ P_{tot} = P_{at} + \rho_{fl} g h \]

Again, \(\rho_{fl}\) is the fluid density, \(h\) is the depth below the surface of the fluid where you are measuring the total pressure \(P_{tot}\), and \(g\) is the magnitude of the gravitational field.

This equation works if you have a container of fluid open to the atmosphere, with only one fluid in it. You can easily imagine a situation where more than one fluid is in the same container. There are many fluids which do not mix, and can form separate layers on top of each other, such as oil and water (how would you know what the order of the layers is, from top to bottom?). In that case, at the bottom of the container, the total pressure would be the sum of all the changes in pressure from each of the fluids, along with the atmospheric pressure, if the container is open. Then,

\[ P_{tot} = P_{at} + \sum_i \Delta P_i = P_{at} + \rho_1 g h_1 + \rho_2 g h_2 + \cdots \]

where \(\rho_i\) is the density of fluid with index \(i\), and \(h_i\) is the total depth of the fluid layer (or how deep the point is within that fluid, for the fluid the measuring point is inside).

One thing you may have noticed is that there was no mention of the container’s shape at all! If the fluid is at rest, then the forces of the container wall on the fluid have to balance the fluid’s force (coming from the pressure) back on the wall, due to Newton’s 3rd law. Thus, the shape of the container does not matter at all when finding the pressure in a fluid, only the depth the measuring point is below the top of the fluid. You can explore pressure at a depth using the PhET linked below.

Problem

The figure below shows four identical boxes held stationary in a pool of water. Which choice below correctly ranks the fluid pressure on the bottom of each block, from greatest to least?

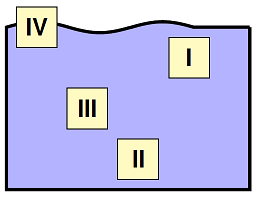
Fig. 15.8 Rank the fluid pressures on each block

Answer: II > III > I > IV

Problem

Water in the lake behind Hoover Dam is 221 m deep. What is the water pressure (aka gauge pressure) at the base of the dam (in MPa)?

Fig. 15.9 Hoover dam seen from the air (source)

Answer: 2.17 MPa

Problem

The Mariana Trench is located in the Pacific Ocean at a depth of about 11.7 km below the surface of the water. The density of sea water is 1025 kg/m\(^3\). If an underwater vehicle were to explore such a depth, what force (in MN) would the water exert on the vehicle’s observation window, with a radius of 13.0 cm?

Fig. 15.10 The U.S. Navy bathyscaphe Trieste, just before her record dive to the bottom of the Marianas Trench, 23 January 1960. The waves were were about 1,5 to 1,8 m high when scientist Jacques Piccard and Lt. Don Walsh, USN, and Piccard boarded from the rubber raft attached to the bathyscaphe. The destroyer escort USS Lewis (DE-535) is steaming by in the background. (source)

Answer: 6.25 MN

15.4.2. The US Standard Atmosphere model

It is important for many applications to have a “standard atmosphere” model, which gives a way to compute the pressure, temperature, and air density of the Earth’s atmosphere at various heights above the surface. In particular, the World Meteorological Organization defines a standard atmosphere as:

…a hypothetical vertical distribution of atmospheric temperature, pressure and density which, by international agreement, is roughly representative of year-round, midlatitude conditions. Typical usages are as a basis for pressure altimeter calibrations, aircraft performance calculations, aircraft and rocket design, ballistic tables, and meteorological diagrams.

I will go through the basic assumptions of the model, then you will try your hand at finding the temperature at a given height using the model. The United States is currently using the US Standard Atmosphere model, last updated in 1976.

To start, the model assumes hydrostatic equilibrium; this is just a fancy way of saying the same pressure-height equation we were using earlier. The only difference is that, since we are now going up in the fluid (i.e. the atmosphere!), it is more convenient to use the height \(r_z\), instead of a depth \(h\). Since we are increasing our height, rather than going downward in depth, we need to take this difference into account by using \(\Delta r_z = -\Delta h\). Again, the minus sign comes from the fact we are moving upward in the fluid, not downward. Thus, our first equation relates pressure \(P\) to the distance \(r_z\) above sea level, or

\[ \Delta P = -\rho g \Delta r_z \]

The second equation is one you probably have seen before in chemistry – namely, the ideal gas law. This relates the pressure \(P\), the temperature \(T\), and the volume \(V\) of a “packet” of gas, based on its composition. Specifically, the ideal gas law is

\[ PV = nRT \]

where \(n\) is the number of moles of the gas, \(R\) is the ideal gas law constant, with \(R = 8.314\) J/(mol K), and \(T\) the temperature of the gas (in K). Notice we are using degrees kelvin, or K, for our temperature measurements. To put this in a more helpful form, let’s write this in terms of gas density, instead of volume, since it is density that appears in the pressure-height equation above. Using the fact that \(n\) is the mass \(M\) of gas divided by the molar mass \(m_{mol}\) of the gas, then with \(M = \rho V\), after some algebra we can solve for density to get

\[ \rho = \frac{m_{mol} P}{RT} \]

This gives us two relations between the three quantities of pressure, density, and temperature. To round out the group, we need some way of finding the temperature at a given height. The US Standard Atmosphere model assumes that, for heights of 11.0 km and below, that the temperature decreases at a steady rate with height. This depends on a constant known as the termperature lapse rate, given by the symbol \(\lambda\). Thus, the third equation is

\[ \Delta T = \lambda \Delta r_z \]

Now, to find the pressure, air density, and temperature at any given height, we need some physical constants and starting values. The values for the US Standard Atmospheric Model are given to four sig figs in the table below; notice that the value of \(g\) slightly different than what is usually assumed in class.

Symbol	Value	Meaning
\(P_0\)	101.3 kPa	Sea level pressure
\(g\)	9.806 m/s\(^2\)	Constant grav. field mag.
\(m_{mol}\)	0.02896 kg/mol	Mean mol. mass of air
\(R\)	8.314 J/(mol K)	Ideal gas const.
\(T_0\)	288.2 K	Sea level temp.
\(\lambda\)	-0.0065 K/m	Temp. lapse rate (up to 11 km)

Notice that the temperature lapse rate is negative, since the temperature decreases for the first 11 km of the atmosphere; however, the air remperature can actually increase for higher altitudes!

Problem

Use the US Standard Atmosphere values for the pressure and temperature at sea level, along with the air density equation derived above, to find the density of the atmosphere at sea level.

Answer: 1.22 kg/m\(^3\)

Let’s take a moment, and think about the equations of the US Standard Atmosphere model, specifically those for the pressure and temperature:

\[ \Delta P = -\rho g \Delta r_z \qquad \Delta T = \lambda \Delta r_z \]

Notice these look a lot like the equations

\[ \Delta {\vec r} = {\vec v}_{avg} \Delta t \qquad \Delta {\vec v} = {\vec a}_{avg} \Delta t \]

we have been using from kinematics to get the motion of objects! In fact, they are a little easier, since pressure and temperature are scalar quantities, not vectors. Thus, we can start at a given height \(r_{z, i}\) and use these equations to find \(P\) and \(T\) at a different height \(r_{z, f}\), by choosing an appropriate height interval \(\Delta r_z\), along with the constants \(g\), \(\lambda\). You will also have to use the ideal gas law to find the atmospheric density \(\rho\) at a particular height \(r_z\), based on the pressure and temperature found at that height.

Problem

Write a Python function findTemp(HEIGHT) that finds the atmospheric temperature at a given height \(r_z < 11.0\) km in the Earth’s atmosphere. The argument HEIGHT of the function should be the height in meters above sea level, and the function should return the temperature in degrees kelvin. Notice that you will have to use only the equation for temperature as a function of height. Thus, you need a loop that updates the temperature values as the height increases. To test your function, you should get 217 K (or -56\(^\circ\) C) when using \(r_z = 11.0\) km, with the standard temperature \(T_0\) given in the table above for \(r_z = 0\) m.

Answer: Here is a possible solution. Notice that the height interval \(\Delta r_z\) is chosen to be 10.0 meters, which gives sufficient accuracy for this application, over distances up to 11.0 km.

def findTemp(HEIGHT):
    '''
    Using the US Standard Atmosphere model,
    find the temperature at a given height above
    sea level on Earth. Assume the gravitational
    field magnitude is constant at all heights.
    '''

    # Physical constants (from US
    # Standard Atmosphere model)
    
    LAMBDA = -6.5E-3        # temp lapse rate (K/m)
    temp = 288.2            # sea level temp (K)

    # Starting height, height interval
    
    r_z = 0                 # m
    DZ = 10                 # m

    # Calculation loop

    while r_z < HEIGHT:

        # Update temperature
        
        temp += LAMBDA * DZ

        # Update height

        r_z += DZ

    return temp

15.5. Pascal’s principle

As mentioned above, for a stationary fluid, the shape of the container does not matter when measuring the pressure at a given depth. Let’s explore this notion some more. We can think of the fluid as composed of imaginary bags, each of which is pressing against its neighbors, or the container walls. In equilibrium, these forces will balance out, and the fluid remains stationary. If they did not balance out, then the net force on each “bag of fluid” would give it an acceleration until the forces did balance out, and equilibrium is restored.

Now, suppose there is an outside force acting on the fluid. This could be something like a piston pressing down on the fluid, or even a change in atmospheric pressure above a lake as a storm front comes into the area. This results in a change in the force on the top of the fluid. The “bags of fluid” will then rearrange themselves to account for this different force, until the fluid is again in equilibrium. Every change in pressure from outside the fluid will result in the same change in pressure everywhere inside the fluid as well, an idea known as Pascal’s principle. One consequence is that the ressure of a stationary enclosed fluid at one vertical height is the same pressure at a different point with the same vertical height. If it were not, the fluid would flow until the pressures are equalized, and the net force on each “bag of fluid” is now zero.

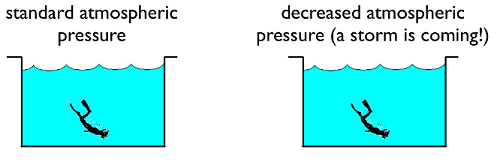
Fig. 15.11 Pascal’s principle says the pressure throughout the pool changes due to an external change in pressure

Let’s go through an example, to see how this principle has practical consequences. Suppose we have a U-shaped tube, as shown in the diagram below, filled with water at the bottom, and oil on one side of the tube.

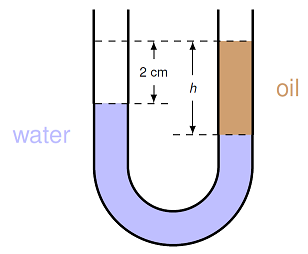
Fig. 15.12 U-tube filled with water

We are interested in finding the height \(h\) of the oil column, if we know that the oil has a density of 800. kg/m\(^3\). We use Pascal’s principle to figure out this distance. Imagine we have two pressure gauges. If we place them side by side at the bottom of the tube, they should read the exact same pressure. Now let’s raise the gauges upward, one of either side of the tube, so that they are always in the same depth of water inside the tube. Because they are in the same fluid at the same depth, they will still read the same pressure. This is true until the gauge going up the right side crosses into the oil; because the oil has a different density, the pressures will now be different on either side of the tube. So, at the highest point where there is still water on both sides of the tube, we can say that the pressures are equal:

\[ P_{left} = P_{right} \]

Now, we need to write out what the pressures are on either side at this particular depth. On the right-hand side, the pressure is due to the atmosphere, and the depth \(h\) of oil above the water; on the left side, it is the atmosphere along with the depth \((h - d)\) cm of water, where \(d = 2.00\) cm is the difference in surface height. This means that saying the pressures are equal on either side of the tube means

\[ P_{at} + \rho_w g (h - d) = P_{at} + \rho_o g h \]

where \(\rho_w, \rho_o\) are the densities of water and oil, respectively. Cancelling out the two atmospheric pressures first, then cancelling out the factors of \(g\), we can solve for the depth \(h\) as

\[ h = \biggl( \frac{\rho_w}{\rho_w - \rho_o} \biggr) d \]

Notice what happens: the depth \(h\) is determined by a ratio of densities, multiplied by the difference in surface depths \(d\). Thus, as long as the units for the densities are the same, the units for \(d\) and \(h\) will also be the same – there is no need to convert! Plugging in the numbers gives \(h = 10.0\) cm.

Problem

Technically, the two atmospheric pressures are not the same on either side, because of the slight difference in the surface height in the tube. Take this difference into account, using the density of air \(\rho_a = 1.22\) kg/m\(^3\) (as you found in a previous problem), and see how much of a change there is in your answer for \(h\). Calculate your answer to four sig figs.

Answer: 9.988 cm (or a 0.122% difference)

Problem

A U-shaped tube is filled mostly with fresh water, but a small amount of vegetable oil has been added to both sides. Calculate the density of the oil in kg/m\(^3\), using the distances \(h_1 = 4.00\) cm, \(h_2 = 9.00\) cm, and \(h_3 = 3.00\) cm.

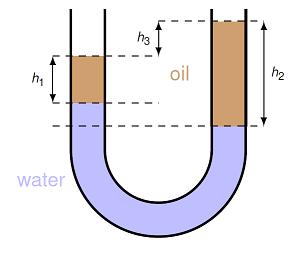
Fig. 15.13 U-tube filled with water and vegetable oil

Answer: 400. kg/m\(^3\)

As a military application of Pascal’s principle, we can look to the action of torpedoes. Torpedoes do not sink ships by holing their hulls, but instead are fired underneath the keel of the target. When the torpedo detonates, it creates a pressure wave, which forms the boundary of a steam bubble, lifting the hull and weakening the keel. The steam bubble quickly collapses, dropping the ship downward and breaking the keel. For more information, see the chapter Underwater Weapons at the on-line Introduction to Naval Weapons.

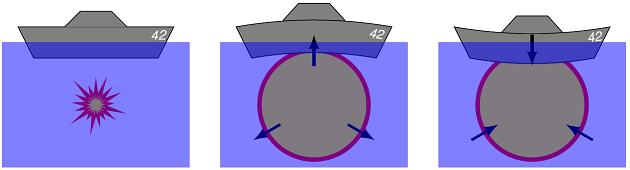
Fig. 15.14 How a torpedo breaks a ship’s keel

In June 1999, the Australian submarine HMAS Farncomb conducted a live-fire sinking exercise against the former HMAS Torrens, a destroyer escort. The video linked below clearly shows the intended effects of a torpedo on a target ship.

15.6. Buoyancy

15.6.1. Archimedes’ principle

We now have the pieces we need to find the buoyancy force on an object in a fluid. Suppose we put a cylinder into a container. The fluid will exert a pressure on all sides of this cylinder. In particular, the pressure is greater on the bottom of the object than it is on the top, because the bottom is at a greater depth. This means there is a greater force \(F_{bot}\) on the bottom surface area \(A_{bot}\) than the force \(F_{top}\) the fluid exerts on the top area \(A_{top}\). The buoyant force will be upward because of this difference. Because we are using a cylinder for simplicity, \(A_{bot} = A_{top} = A\); we can do the same thing for more complicated shapes, but it requires more math. In addition, the forces on the side will not matter, since the forces on opposite sides of the cylinder middle will cancel out.

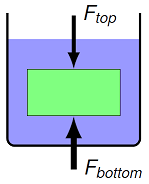
Fig. 15.15 Forces acting on a completely submerged object

Now, suppose the top of the cylinder is at a depth \(H_{top}\). If the cylinder has a height \(h\), then the bottom of the cylinder will be at a depth \(H_{bot} = H_{top} + h\). Let’s use this to find the net force on the cylindrical object, due to the fluid. Using the relations between force and pressure, and the method to find pressure at a depth, we have

\[ \sum F_y = F_{bot} - F_{top} = (P_{bot} A) - (P_{top} A) = (P_{at} + \rho g H_{bot}) A - (P_{at} + \rho g H_{top}) A \]

Cancelling out the common atmospheric pressures, we get

\[ \sum F_y = \rho g (H_{bot} - H_{top}) A = \rho g h A \]

However, the quantity \(hA\) is just the volume of the cylinder; I will call this \(V_{disp}\), the volume of fluid displaced by the object. This may not be the same as the object’s volume, if it is not completely immersed! So the net force of the fluid on the object, which we call the buoyant force \(F_B\), is given by

\[ F_B = \rho_{fl} g V_{disp} \]

There are a couple of important things to note here. The density \(\rho_{fl}\) is the density of the fluid, not the object. Remember that this came in because we found the forces on the object due to being at a depth in the fluid. The volume \(V_{disp}\) is the volume of the object in the fluid. For the derivation above, we assumed that the object is completely submerged, but it also works for partially submerged objects, i.e. when the top is outside the fluid.

Because of these facts, the combination \(\rho_{fl} V_{disp}\) is actually the mass of the fluid pushed aside by the object, so \(\rho_{fl} g V_{disp}\) is the weight of the displaced fluid! This gives us a derivation of Archimedes’ principle, stated next.

Archimedes’ principle

An object immersed (either completely or partially) in a fluid experiences an upward buoyant force equal in magnitude to the weight of fluid displaced by the object.

Problem

Imagine holding two identical bricks in place under water, as shown in the diagram below. Brick 1 is just beneath the surface of the water, while brick 2 is held about two feet down. Fill in the blank in the following sentence: “The force needed to hold brick 2 in place \(\underline{\hspace{2cm}}\) is the force for brick 1.”

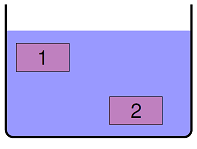
Fig. 15.16 Two immersed blocks

1. greater than

2. less than

3. equal to

Answer: Each of the bricks have the same volume, and are in the same fluid. Thus, the buoyant and gravitational forces on both are the same. This means you need the same applied force to hold each in place.

Make sure you keep track of your quantities

Here is some advice when finding the buoyant force using Archimedes’ principle. This idea is very powerful, but you also need to be very careful about the quantities involved. Typically, you know the density of the fluid, and maybe the density of the object as well. You may also know both the total volume of the object, and the amount of this volume that is in the fluid (e.g. for a floating object, these will be different). You need to make sure that you are matching the right quantities when finding the weight of the displaced fluid. This will depend on the fluid density, and the volume of fluid displaced by the object. This will give rise to a force on the object, which has its own density and total volume. Don’t get these mixed up!

To see an example of this, let’s imagine we have a spherical balloon with a diameter of 4.80 m. The skin of the balloon is made of neoprene synthetic rubber, and has a mass of 1.08 kg. The balloon is filled with 30.0\(^\circ\) air, with a density of 1.16 kg/m\(^3\), and the air outside the balloon is at room temperature (20.0\(^\circ\)) with a density of 1.20 kg/m\(^3\). If you want to put an electronic instrument onto the balloon as cargo, what is the maximum mass it could have?

First, notice in this problem there are several densities: the inside air \(\rho_{in}\) = 1.16 kg/m\(^3\) and the outside air \(\rho_{out}\) = 1.20 kg/m\(^3\). It is the outside air that acts as the fluid in which the balloon is completely immersed; this will be our \(\rho_{fl}\) in the equations above. On the other hand, the inside air is part of the system, so it will contribute to the total weight of this system – air has a weight! Thus, the total weight of the balloon-inside air system include the cargo \(F_{g, cargo}\), the skin \(F_{g, skin}\), and the inside air \(F_{g, in}\) (all downward), while the upward buoyant force \(F_B\) results from the pressure of the outside air on the balloon skin. It is the small difference in density between the inside and outside air that allows a buoyant force, lifting the balloon itself along with its cargo. Thus, the FBD for the balloon looks like

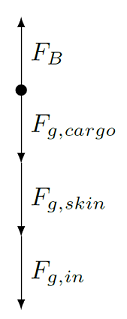
Fig. 15.17 FBD for the balloon

Starting from Newton’s 2nd law

\[ \sum F_y = F_B - F_{g, cargo} - F_{g, skin} - F_{g, in} = m_{tot} a_y \]

we use the gravitational and buoyant force equations as appropriate:

\[ \sum F_y = \rho_{out} g V - m_{cargo} g - m_{skin} g - \rho_{in} g V = m_{tot} a_y \]

Here, \(V\) is the volume of the spherical balloon. The volume of a sphere of radius \(R\) given by \((4/3) \pi R^3\), and the radius \(R = 2.40\) m is half the diameter. Thus, the volume here is \(V = 57.9\) m\(^3\). The balloon will rise into the air only if \(a_y \ge 0\). Thus, we need to find the cargo mass \(m_{cargo}\) that gives

\[ \rho_{out} g V - m_{cargo} g - m_{skin} g - \rho_{in} g V \ge 0 \]

Dividing by \(g\) does not change this inequality; solving for the cargo mass gives

\[ m_{cargo} \le (\rho_{out} - \rho_{in}) V - m_{skin} \]

The maximum cargo mass is equal to the right-hand side, i.e. when the inequality becomes an equality. Plugging in the numbers gives \(m_{cargo, max}\) = 1.24 kg.

15.6.2. Floating objects

Obviously, one important application for Archimedes’ principle in the sea services is making sure that ships remain afloat (and submarines can maintain cruising depth). In this case, the net force on the ship must be zero, which means that the buoyant force is the same as the ship’s weight.

Fig. 15.18 Forces acting on a floating object

For this to happen, the floating object is in equilibrium, so forces balance:

\[ F_b = F_{g, obj.} \]

By Archimedes’ principle, the buoyant force is equal to the weight of the displaced fluid:

\[ F_b = F_{g, fluid} \]

Putting these equations together gives for a floating object that

\[ F_{g, obj} = F_{g, fluid} \]

Thus, a floating ship must displace exactly its weight in water in order to stay on the surface. This is why, instead of giving the ship’s mass, this statistic is listed as the ship’s “displacement” (in tons, usually). For submarines, you may see two different displacements – surface and submerged. The first, like that of the ship, gives the amount of water equivalent to the sub’s mass; the second gives the amount of water with the same volume as the sub. Which would you expect to be bigger?

Problem

Two identical blocks are floating in two separate aquariums. Aquarium A is filled with alcohol (\(\rho\) = 789 kg/m\(^3\)), while aquarium B is filled with pure water. Which has the greater buoyant force acting on it?

1. The block floating in alcohol

2. The block floating in pure water

3. They both have the same buoyant force

4. Cannot determine without the density of the blocks

Answer: The key word here is floating. Since both blocks are floating, then the buoyant force acting on each is equal to each block’s weight. Since the blocks are identical, the two buoyant forces must be the same! However, the block in alcohol will float deeper in the fluid to get the same buoyant force; this is the only different between the two situations.

Problem

You are shopping online for a new barge at McDonough Marine Services, and settle on a 140’ \(\times\) 40’ \(\times\) 9’ 6’’ size barge. First, some helpful information. The freeboard is the distance from the deck of the barge down to the water line. The loadline is the freeboard when the maximum safe cargo is placed on the barge, so that it is the highest water line for safe operations. A metric ton (mt) is 1000 kg.

Fig. 15.19 The Occitania and a 2,500-ton barge carrying a load of coal destined for a thermal power plant (source)

Looking on the website, you see that the you can load 965 mt of cargo when the water is at the loadline; the following table gives the safe amount of cargo for various values of the freeboard.

Freeboard	Cargo (mt)
3’	820
4’	660
5’	550
6’	340

1. What is the mass of the barge in metric tons? Use a density of 1010 kg/m\(^3\) for sea water.

2. Where is the loadline located on the barge? Give the distance in cm from the barge deck.

Answers: 220 mt; 63.6 cm, or just under 2’ 11”

Here’s another example to work through. Suppose you have a cone with a given density \(\rho_{cone}\); the top of the cone is a circle with a radius \(r\), and the cone has a total height \(h\). You place the cone in a fluid of density \(\rho_{fl}\), and it floats. How far down into the fluid does the cone sink before coming to rest? First, we need to know the volume of a cone, which is

\[ V_{cone} = \frac{1}{3} \pi r^2 h \]

It is important to note that the amount of fluid displaced by the cone when it is a depth \(h_{fl}\) in the fluid is proportional to this. Hopefully it is clear from the picture below that the ratio of the total radius \(r\) and height \(h\) of the cone is the same as the radius of the cone \(r_{fl}\) and the height of the cone \(h_{fl}\) that is immersed in the fluid. In other words,

\[ \frac{r}{h} = \frac{r_{fl}}{h_{fl}} \]

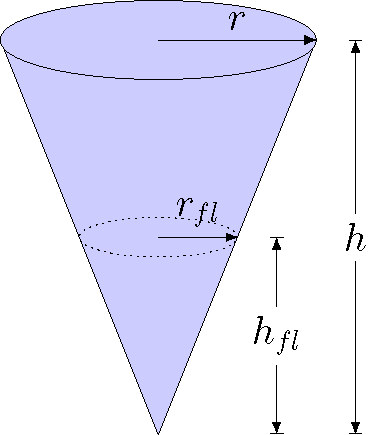
Fig. 15.20 The radii and heights for the floating cone

Now, let’s use these facts to find out where the “water line” of the cone is, i.e. what depth \(h_{fl}\) is immersed in the fluid. Since the cone is floating, then \(F_{g, cone} = F_B\). Thus,

\[ m_{cone} g = \rho_{fl} g V_{disp} \]

The mass of the cone is given by the density of the cone times its total volume; the volume displaced is given by the volume of the cone under the water line, which is a distance \(h_{fl}\) from the cone’s tip. Substituting these into the force equation above,

\[ \rho_{cone} g \biggl( \frac{1}{3} \pi r^2 h \biggr) = \rho_{fl} g \biggl( \frac{1}{3} \pi r_{fl} ^2 h_{fl} \biggr) \]

We can cancel out some common factors here. We can also use the fact that \(r_{fl} = (h_{fl} / h) r\) to eliminate the radius \(r_{fl}\); this substitution will also allow us to cancel out \(r\). Putting all of this together, we have that the depth \(h_{fl}\) of the cone in the fluid depends only on the total cone height \(h\), and the ratio of the fluid and cone densities:

\[ h_{fl} = \biggl( \frac{\rho_{cone}}{\rho_{fl}} \biggr)^{1/3} h \]

Obviously, this is sensible, as we can see with two test cases. If the two densities are the same, then the cone will be completely immersed in the fluid. For the opposite case, as the cone density gets very small, then very little of the cone will be immersed in the fluid. In between, most of the cone’s volume is away from the tip and towards the base. This means that, for example, if the cone has half the density of the fluid, then almost 80% of the the cone must be in the fluid! There is very little cone volume near the tip, so the cone must be more than halfway in the fluid to get the forces to balance out.

Problem

An iceberg has a density of 917 kg / m\(^3\) and is floating in sea water (\(\rho = 1025\) kg / m\(^3\)). What fraction \(V_{sub} / V_{tot}\) of the iceberg is submerged in the sea water?

Fig. 15.21 An iceberg in the Arctic Ocean (source)

Answer: 0.895

15.7. Summary

Fluids are an important topic for those in the sea services. It can also be challenging to think through some of the puzzles you encounter with buoyancy. To emphasize the point: this is one of those topics where you really need to think through the consequences of the definitions and Archimedes’ principle. Some of these consequences may be counterintuitive!

After this lesson, you should be able to:

• Define pressure, and identify its units (SI and otherwise).

• Use the definition of pressure to find an unknown force or area.

• Define atmospheric and gauge pressures.

• Find the pressure on an object at a certain depth inside of a fluid

• Use Pascal’s principle and the relation for pressure at a given depth in a fluid to find the height or density of a fluid in a U-tube.

• Describe the relationship between the portion of an object’s volume in a fluid, and the amount of fluid displaced by that object.

• State Archimedes’ principle.

• Use Archimedes’ principle to find the amount of an object that is immersed in a fluid.

14. Inclined planes 16. Circular motion