.ipynb .pdf

Binder

Contents

1. Introduction to Python

1.1. Overview

Links to programs in this lesson:

1. ‘Hello world!’

2. Defining variables

3. If statements

4. While loops

5. For loops and range()

6. For loops and lists

7. firstFiveMultOfSeven()

8. multipleSum()

9. Heron’s method

10. squareRoot()

In this lesson, you will learn the basics of the Python programming language. You will use this in subsequent lessons to explore some of the foundations of physics; I hope you have fun creating these simulations on your computer! Python was invented in 1990 by Guido van Rossem, a Dutch computer scientist. Python is a modern, object-oriented language which is easy to learn. All of the instructions you give the computer will be in the Python programming language. These instructions are collectively called code.

Why are we doing this?

• Physics uses tools from many other different areas – writing, mathematics, and more recently, computer programming. Nowadays, any working scientist, mathematician, or engineer should know at least the basics of writing a computer program.

• In Python, we can create simulations that illustrate what is happening in physical situations. This helps to understand aspects of physics that are difficult to see using other methods.

• Both physics and computer programming involve thinking logically about a problem, and solving it in a methodical way. In particular, you must understand the physics concepts yourself before you can explain it clearly and precisely to a computer!

• An important skill in programming is learning how to debug a program – figuring out where in the program code a mistake has been made, and fixing it. Sometimes this can take a while! A similar skill is very useful in finding the error in a physics problem solution.

Why Python?

• Python is very common language that is relatively easy to learn, but has lots of add-ons for powerful applications.

• There are several physics classes across the country that use Python programs in their class.

• We will often use the vPython package, which allows us to easily create 3D visuals.

This lesson goes through some of the basic concepts and Python commands we will need to study the motion of objects.

Trying the code

The only way to learn anything in life is to try it yourself. Watching another person do something does not teach you anything; you have to do it yourself.

With this in mind, these lessons are written specifically so that you can work through them interactively when you are using the online version at https://dcartin.github.io/. As you look through the pages of the online book, you will see programming code embedded on the site, using a website called Trinket (https://trinket.io/). When you get to these programs, it is strongly recommended you not only run them, but also modify them to see how they work.

For this course, you will complete programming assingments based on what is covered in this lesson and the following one (Lesson 02). To do this, you should create an account (for free) on Glowscript.org. You may want to use your personal email account, so you can modify these programs after you leave NAPS.

As you read through this lesson, you should keep in mind the specific objectives I hope you achieve. Every lesson will have such a list, and these lists also appear in the course syllabus. You should read through the objectives carefully first thing – don’t skip it! Below is your checklist for this lesson, the things you should get out of your reading:

• Print the value of a numerical variable or a string to the screen using the print statement.

• Create a Python program.

• Define a variable, and state the rules for Python variable names.

• Add a comment to a program.

• Update the value of a numerical variable.

• Use the mathematical operators +, -, *, /, % to calculate the new value of a variable.

• Use an if statement to check whether a logical condition is true.

• Use a while loop to implement statements until a logical condition is false.

• Create a list of values.

• Select a specific value from an existing list.

• Create a function with specified arguments that returns a desired quantity.

There are a lot here, but most are relatively short. This lesson is also an important foundation for all of the Python we will use in the course, so I put it all in one lesson! If you don’t feel you can do these things, you should work at it – did you miss an important definition? Try the problems? Maybe playing around with the code examples more, and thinking of different scenarios will help. Remember, the online version of this textbook at https://dcartin.github.io/ has interactive versions of these programs.

1.2. The print command

For those learning a new programming language, it is traditional to first learn how to print the statement “Hello world!” This is known as a string, as opposed to an integer such as 5 or a floating point number (or float) such as 3.141592654. Together, these are known as data types.

Below is our first piece of code. On the left, you will see the Python command print(), which tells the computer to print whatever is inside the parentheses. In this case, the command will print the string 'Hello world!'. Run this short program by clicking on the right-facing arrow in the upper-left corner of the Trinket app window.

Back to program list

If the computer prints Hello world! in the right-hand window, then congratulations – you’ve just run a Python program!

If you didn’t try to run this program, try it now! These lessons are meant to be interactive – play around with them, try different possibilities, and see what works and what doesn’t. One advantage of programming is you can see what the consequences are of various choices. What gives you natural looking simulations, and what gives you “bad physics”? You will learn best by trying.

I will be using these Trinket apps a lot over the course of the lessons, so this is a good place to acquaint you with some of the available features. I have highlighted these in Figure 1.1 below. Hopefully, you have already tried the arrow button to run the code. This will run the program code shown on the left-hand side of the app; this code may be long, so you can scroll down this side if necessary. In addition, there is a fullscreen option, which you can find by clicking on the three horizontal lines in the top left corner. On the right, the default will be to show a description, and any instructions, going along with the program. When you run the program, this will shift to the results of the program run. You can always switch back and forth between the results and the instructions by clicking the appropriate tab on the right-hand side. Finally, if you are interested, you can create your own Trinket.io account; this will allow you to save and modify programs you find throughout the lesson.

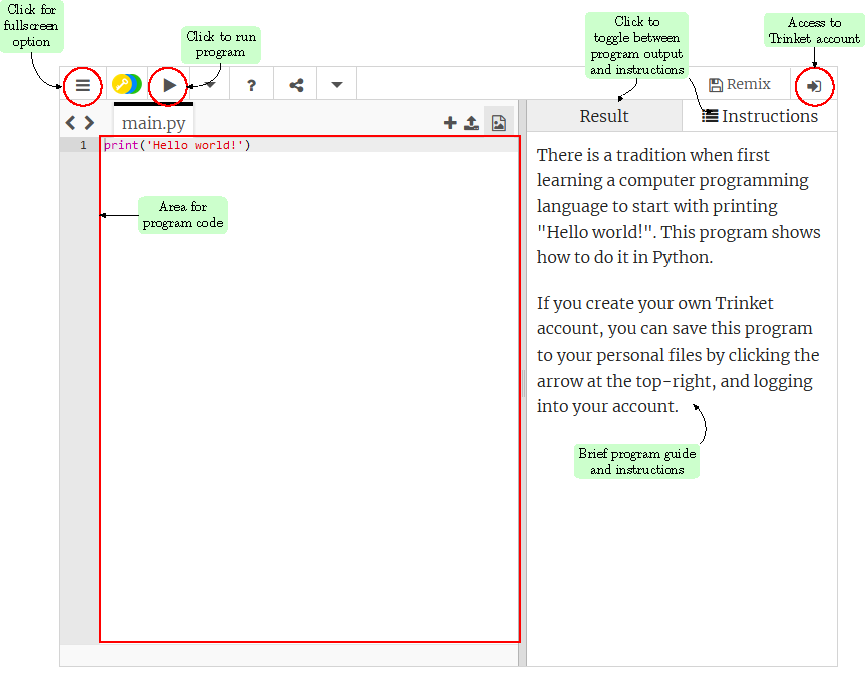
Fig. 1.1 Some of the features of the Trinket app

Now, let’s get back to some Python programming. You should be careful what kind of quote marks to use when writing strings. For example, the marks above are those on the right-hand side of the keyboard, not those at the upper left. Try using those, and see what happens. If you change the command in the program above to read

print(`Hello world!`)

the Trinket app will show an error message at the bottom of the window.

Note that using double quotes at the beginning and end of the string will also work. Try changing the program above so it reads

print("Hello world!")

and run the program again. The reason for this is if you need to use single or double quotes inside the string you want to print. An example would be

print('Who says "Hello world!" anymore?')

However, you can’t mix single and double quotes at the beginning and end of the string. If you change the code above to read

print('Hello world!")

you should get an error. Whenever you get an error like this, you can go back and edit the program so that it works properly.

Problem

Try intentionally putting mismatched quotation marks in the Trinket app above, and run the program. What happens? Then change the code back to proper format, and run the program again.

Answer: The computer should give you an error message, such as “SyntaxError: bad token on line 1 in main.py”.

---

Often, you will notice that, right after a problem, there is a “plus” icon, along with the text “Click to show”. Clicking the icon will show the answer to the problem! Click on the icon again (now a “minus” sign) to hide the answer.

1.3. Variables and mathematical operators

Many times we need to store numerical values for use later on in the program, and change these values as the program progresses (e.g. think about the position of a moving object). This is done in programming languages by creating a variable and setting it equal to the value desired.

A variable is given a name when it is defined, and every time you want to change or modify the variable, you can do so by using that name. The rules for variable names in Python are

• The variable name must start with either a letter or the underscore (_) character. However, it is probably not a good idea to start with the underscore, since variable names like these are usually reserved for important things that run Python!

• Variable names cannot start with a number.

• Variable names are case sensitive, so var, Var, and VAR are three separate variable names.

• Variable names can only use letters, numbers, and the underscore.

I also use the convention that constants are given names in all capital letters. These will indicate variables that should not be changed anywhere in the code. So, if I want to define the total time a simulation will run, I may call it MAX_TIME. On the other hand, the current time could be another variable, such as t, which does change. I also tend to put the definitions of all the variables at the top of the program, so I can find them easily if I need to alter their values.

Here is a Python example, creating the variable position and giving it a value of 5. The print statement verifies that the variable is set correctly. You will use this program for the rest of this section.

Back to program list

You will notice there are extra pieces to the program above – lines starting with the character #, and which are not Python commands. These are known as comments. With longer programs, it helps to add in comments in English that the computer does not try to read as commands. For example, with the code

x = 5     # Sets value of the variable 'x'

the computer will not read anything beyond the # symbol. You will see the program above has some comments in it, to explain what is happening in the code. Good code features comments, so that if it is read by someone else (or you, sometime in the future!), there is a lot of explanation of how the program works. This becomes more important as your code gets more complicated. You should get into the habit of including comments to both explain the programming code itself, and as notes to understand the variables. For example, one comment may say a particular part of the code is creating the motion of an object in the simulation; another comment may tell the reader that the SI units for the variable velocity are m/s.

Problem

What is the result of running the following code?

x = 5     # x = 7
print(x)

Answer: The computer will print the number 5.

Now let’s get back to talking about variables. What happens if we run the statements given below? Change the program above so it looks like this code now.

position = 5
print(position)
position = 7

Is the answer what you expected? The computer will run the statements in order, starting from top to bottom, unless the order is changed by other commands.

Do I have to do it this way?

This method of printing the value of position shows that Python cares about the type of the variable; different types will be treated differently. This will be important later, when we start talking about vectors in vPython. Mathematically, vectors are not the same as numbers, and knowing what operations you can use them for will be a crucial skill for this class.

That being said, there are other ways of printing the values of numerical variables in Python. If you know what they are, great! But what results they give can depend on the version of Python you are using; this is not a critical thing to know, so I don’t want to worry about it too much.

We can also print the name of the variable (as a string) along with the value of the variable. Add the command

print('position = ' + str(position))

below the command position = 7. Notice that two things are going on here: the computer is converting the integer position into a string, then it is combining this string with the string 'position = ' by “adding” the strings. Putting this together, the computer should print position = 7, so you can see the name of the variable, along with its value. As we get into more complicated programs, using print statements can help debug the program, if something doesn’t go quite right, or you get error messages.

Now that we have seen we can store numerical values in variables, we can now use mathematical operations on these variables. Below is a list of the common ones.

Operation	Python symbol
addition	+
subtraction	-
multiplication	*
division	\
remainder	%
exponentiation	**

Note that ^ is not a symbol for exponentiation in Python! Thus, if you want to find 2 * 2 * 2, then in Python it is 2 ** 3 and not 2 ^ 3. As an example of a mathematical operation, add the lines given below into the program above, under the appropriate comment. Then run the program to see the result.

x = 5
y = 7
print(x * y)

Problem

In the above program, change the * to the other four mathematical operators, and make sure the answer is what you expect.

Problem

Write a Python program that defines a variable number, then prints out the value of three times the original number plus one. Print this new value out.

Answer: Here is a possible program, starting with the number 17.

number = 17
print(3 * number + 1)

1.4. if statements

Our short-term goal is to learn enough Python programming to simulate the motion of an object, such as a ball; you will do this in Lesson 02 (velocity and vPython). Suppose we want to check whether the ball has hit the ground or a wall. In Python, this requires the use of an if statement. This will check to see if a certain condition is true. If it is, the next indented lines will be executed. Otherwise, the computer will move to the next line that is not indented and continue from there. Consider the code in the Trinket app below; you will use this program for the rest of this section. Notice that the colon : is important – it tells the computer the if statement is done. Again, everything that is indented below the if statement will be run if the if statement is satisfied.

Back to program list

Problem

In the program above, change the definition of nextNum to 7, then run the code again. What happens?

Answer: The computer will produce no output, since the condition nextNum < 5 is not true.

Sometimes we want to do something special if the if statement is not true. We can do this using an else statement, as seen below. Change the program above to match the lines given below, then run the new program.

nextNum = 7
if nextNum > 5:
    print('nextNum is greater than 5')          # nextNum is larger than 5
else:
    print('nextNum is not greater than 5')      # nextNum is not larger than 5

Problem

Change the definition of nextNum to 3 in the program above, and run the code again. What output do you get? What if nextNum is changed to 5? Are the results what you expect?

Answer: When nextNum is changed to either 3 or 5, the output is nextNum is not greater than 5. Note that \(5 > 5\) is not a true mathematical statement!

There are other tests we can do between two numbers:

Symbol	Definition
>	greater than
>=	greater than or equal
<	less than
<=	less than or equal
==	equal to
!=	not equal to

We can use these to modify the program above. Suppose we don’t want to include the case when nextNum is equal to 5, but just less than 5. Then we can use an elif (short for “else if”), as shown below.

nextNum = 7
if nextNum > 5:
    print('nextNum is greater than 5')          # nextNum is larger than 5
elif nextNum < 5:
    print('nextNum is less than 5')             # nextNum is less than 5

This allows us to be more specific; if you modify the code and run it, the computer will print out something only if nextNum is not equal to 5.

Note that there is a difference between setting the value of a variable, and comparing two variables. For example,

z = 3

sets the variable z to an integer value of 3 (defining the variable), while

if z == 3 then:
    print('Yes!')

checks to see if the variable z is equal to 3 (testing the variable). Thus, a single equals sign defines a variable, while a double equals sign checks to see whether something is true. This may be a little confusing, but hopefully you will learn the difference after some practice.

To look at using these testing operations, take a look at this code.

x = 5
y = 4
if x <= 4:
    print('x is less than or equal to y')
else:
    print('x is greater than y')

What would you expect if you ran this code? Make a guess first, then add these lines after the appropriate comment in the program above. If you run this now, what does the computer print out?

Problem

Change the definition of the variable y above, so that \(y = 7\). What result do you get when you run the program?

Answer: The computer will print out x is greater than y.

Problem

After you have added the code listed above, change the if statement so it says “if x <= y:”, then run the program. How well does the code work if you change y to other numbers?

Answer: The output should now be correct for all values of x and y.

Writing Python statments like this – where the if statement checks other variables, rather than numbers – can make the code easier to modify if necessary. Going back to constants, I could use an if statement to see if the current time t is greater than or equal to the constant MAX_TIME I set as the maximum time for the simulation.

Problem

Write a Python program that defines a variable checkNum, then checks to see if the number is zero or positive. If the number is zero, then the computer should print The number is zero; if the number is positive, then print The number is positive. If the number is negative, the computer should not print anything.

Answer: Here is a possible program, starting with the number -3. Note that the if statement only checks if checkNum is equal to zero, or if it is greater than zero. If checkNum is equal to negative (as defined here), neither test is true, and the computer prints nothing.

checkNum = -3
if checkNum == 0:
    print("The number is zero")
elif checkNum > 0:
    print("The number is positive")

1.5. Loops and lists

When writing programs to simulate the motion of objects, we will frequently need to tell the computer to do the same operation repeatedly. For example, suppose we want to show the motion of a falling object. This will involve finding the changes in position and velocity over and over, as time progresses. Thus, we need to loop over the same commands. There are two ways to do this in Python: the while loop and the for loop.

The while loop will execute a series of commands as long as a certain condition is true. This will be very helpful when we are not sure when we want to stop the loop. Suppose we wanted to look at the motion of a projectile launched at some angle, but we included air resistance. How long does it take to reach the ground? It is not easy to tell without running the program! However, we can easily tell the computer to stop the loop when the projectile reaches the ground. This is an example of a condition we use with a while loop.

The code below shows a while loop, where the code will (1) print the value of the variable nextNum, and then (2) add one to nextNum. However, once nextNum is not less than 5, the loop will stop. This means that 4 is the last number printed. The program will then move on to the next line if there is one. Since there isn’t one here, the computer stops.

Back to program list

Just like the if statement, the colon and indentations are important! The computer needs a way to know what statements are inside the while loop.

Problem

Try experimenting with the code above. Here are some things you can try:

• Switch the order of the two commands inside the while loop, so that the statement nextNum = nextNum + 1 comes first.

• Change the while statement so that there is a different number than 5.

• Change nextNum = nextNum + 1 so that it adds a different number than 1.

• Remove the print statement from inside the while loop, and put it after the loop. Note this means that it is not indented, and after the statement nextNum = nextNum + 1. Note that you can use this to print out only the last number, rather than all of the numbers, if you wish.

What this code means

If you are new to programming, the statement nextNum = nextNum + 1 may look very odd indeed. This does not mean something like \(x = x + 1\).

In a Python program (and in many other computer languages), the equal sign means ‘assign a value to this variable’. So the statement nextNum = nextNum + 1 really means: (1) Find the location in memory where the variable nextNum is stored. (2) Read in this value. (3) Add one to this value. (4) Store the result back in the location in memory where nextNum is stored.

In Python, there is a shorthand way of writing code such as nextNum = nextNum + 1. This is given by nextNum += 1. You can read the symbol += to say “read in the quantity to the left, add to it the quantity to the right, and put that back in the location of the original variable”. Writing it like this saves some room in the code, so try to use it if you can! There are other versions for subtraction, multiplication, and division.

Problem

What would your computer print out if you ran the code shown below?

x = 5
x -= 3
print(x)

Answer: The computer will print out the number 2.

Problem

Write a Python program that prints out all multiples of seven that are less than 60, starting with 7.

Answer: One way to do this is given by the program below. The variable nextMult stores the value of the next multiple to print. Inside the while loop, the next multiple is printed, then 7 is added to it, to get the next multiple.

nextMult = 7
while nextMult < 60:
    print('nextMult = ' + str(nextMult))
    nextMult += 7

Now let’s come back to loops. A for loop is a similar idea to a while loop, but in this case, we have a definite idea of how many steps we are taking. Let’s look at some examples of how this would work. Suppose we want to add up the integers from 0 to 5. We would do this by finding \(0 + 1 + 2 + 3 + 4 + 5\). Notice that we counted over six numbers total – this will be important in a second. A possible way to do this in Python is to use the code below.

Back to program list

If you run the code, you should get the result of 15. The for loop ran over the range of the first six integers, starting from zero. This is why it is range(6), rather than range(5), since the range is over six numbers. Unfortunately, the fact that Python starts with zero can be a little confusing sometimes; it has its advantages as well, but watch out that you don’t make a mistake!

Problem

Change the code above so that the sum is over the first 1500 integers, starting from 0. What is the value of the sum?

Answer: You would need to change the code to the following.

total = 0                   # Variable to store sum of integers

for iii in range(1500):     # <-- Here is the change
    total += iii            # Add iii to variable total
    
print(total)

You should get 1,124,250.

Problem

Write a Python program that finds the product of the first ten multiples of 13.

Answer: Here is one possible program. Notice that the variable product used to keep the running value must start as 1, not 0, so you don’t get zero for the final result!

product = 1           # total product
nextMult = 13         # next multiple of 13 to multiply to product
numMult = 10          # number of multiples to combine

for iii in range(numMult):
    product *= nextMult
    nextMult += 13
    
print('product = ' + str(product))

Another way to use a for loop is to use it with a list. A Python list is simply a collection of values, where the order is important. A list is defined by using square brackets, such as

myList = [4, 3.14, "I love my list", -7]

This list has four elements, and as you can see, it can store all kinds of values in the same list. You can access the list by giving the index. An index is a number giving which element of the list a particular member is at, starting from zero. So, for example, myList[0] takes the list myList and sees what is at index 0 (i.e. the first value in the list). Thus, if you run

print(myList[0])

the computer will print out 4. However, if you try

print(myList[4])

you will get an error, since the indices of the list run from 0 to 3 (four entries total). The last entry in the list would be myList[3] instead.

Negative indices

Another way to find the entry in a list is to count backwards from the end. Thus, myList[-1] is the last entry in the list (namely -7), while myList[-2] is the second to last, and so forth.

You can create a list either by just typing it in, as we did with myList above, or by creating it from scratch. Let’s use a for loop like we did above to do this. The code below will create a list of the first six integers. It does this by first telling the computer that intList will be a list. Remember to do this! The computer doesn’t know that intList is a list until you tell it; it could be a string, or an integer, or anything else. Then, we add values to the end of the list using the += operator. Notice that what are adding [iii] to the list – the square brackets match up with the fact intList is a list. You can see this when the list is printed out at the end.

Back to program list

We introduced lists as another way of using a for loop. Instead of using range as above, we can also create a list with a for loop, then use a second such loop to print out the results. Thus, instead of using the print statement, we could have used

intList = []

for iii in range(6):
    intList += [iii]
    
for jjj in intList:
    print(jjj)

The second for loop now prints out the values in intList, only one at a time. Thus, you have now seen two different ways to set up a for loop: either using the range() over a fixed number of integers, or by using the values of a list.

Problem

Define a list that includes all of the personnel in your chain of command, starting with the most senior and working your way down. Do this by typing in the entries by hand into the list, in between square brackets, to create the list. Then print out each of these people, one per line, in the order given in the list.

Hint: Your list is bound to get long, so you probably want to write it on more than one line. However, Python needs to know that you are doing this! To do so, you can add a \ (backslash, not a forward slash) at the end of each line, which tells Python to keep reading the code as one single command. For example, you can change

sampleList = ['really long string', 'another really long string']

into

sampleList = ['really long string', \
              'another really long string']

Answer: Here is a program that creates a list, then prints out, my own chain of command when I first reported to NAPS.

chainList = ['President George W. Bush', \
            'Secretary of Defense Donald Rumsfeld', \
            'Secretary of the Navy Hansford T. Johnson (acting)', \
            'Chief of Naval Operations Admiral Vern Clark, USN', \
            'Superintendent Admiral Rodney P. Rempt, USN', \
            'Captain Bruce Bole, USN', \
            'Lieutenant Colonel Danny Ray, USMC', \
            'Dean Stephen Arendt', \
            'Professor Clarice Anderes']

for person in chainList:
    print(person)

1.6. Procedures and functions

We have now gone through essentially all of the Python commands you will use for this course. In Lesson 02, we will introduce some special commands that help us create simulations, with the vPython module. However, before we get to that, there is one last aspect of Python programming to learn. This is not a new command, but instead is a different way of packaging what we have already done.

As programs become longer and more complicated, it can be difficult to understand what the program is actually doing. Thus, what programmers will do is take pieces of code, and “call” these pieces in the main program when they need them. In other words, the steps that the program is to execute are divided into smaller bits, which are easier to understand and fix if something goes wrong. These pieces are known as procedures and functions. There is a slight difference between the two, which I will explain later, but they basically do the same thing.

Functions and your homework

When you create programs for homework assignments, you will use functions to do so, so make sure you understand everything in this section!

Let’s start with a simple example. Suppose you wanted to find the sum of the multiples of some number, up to a maximum value. To make it definite, let’s say you want the sum of the first MAX_NUM_MULTIPLES of a number NUMBER. You could create a program with variables MAX_NUM_MULTIPLES and NUMBER. I put these variable names in capital letters, because they are not going to be changed in the program. This would look something like the program below; you will later add some code to this program.

Back to program list

Let’s walk through this code, to make sure you understand what it does. First, we define NUMBER to be the number we are finding the multiples of, then total will be the variable where we store our values as the program runs. We count the number of times we have added a multiple to the sum as the variable numMultiples, and set the maximum number of such additions as MAX_NUM_MULTIPLES. Inside the while loop, we increase the number of multiples by one everytime we add a multiple of NUMBER to total. When we have gone over the number of multiples we want, we quit the while loop, and print out the final answer. Since this sum is \(7 + 14 + 21 + 28 + 35\), then the answer is 105.

The example code above would then give you the sum of the first five multiples of 7. Now, suppose you want to calculate this number repeatedly in your program. You could copy the code over and over, but that is a pain. Instead, we create a procedure firstFiveMultOfSeven(), which every time we run it, it goes through the same code and prints out the result. This is given by the code below; notice that it is not very different from the program above, except for the first line. The def command tells Python to create the procedure with our given name firstFiveMultOfSeven(). By the way, I will often put parentheses after the name of a procedure or function when I describe it, so you know it is not a variable.

def firstFiveMultOfSeven():
    NUMBER = 7                     # Number to find the multiples of
    total = 0                      # Sum of all the multiples of NUMBER
    
    numMultiples = 0               # Number of multiples summed so far
    MAX_NUM_MULTIPLES = 5          # Maximum number of multiples to sum
    
    while numMultiples < MAX_NUM_MULTIPLES:

        numMultiples += 1
        total += numMultiples * NUMBER
        
    print(total)                   # Print sum

Modify the program in the Trinket app, so it looks like the procedure firstFiveMultOfSeven() given directly above. Then run the program. Nothing will apparently happen! The computer now knows what to do when you ask it to use this procedure.

Once you define the procedure, you can use anytime you want. To see this, uncomment the line

firstFiveMultOfSeven()

and run the program again. It should print out 105.

However, if I want the first eight multiples of 15 instead, I’d have to go back to the code, and change both the variables NUMBER and MAX_NUM_MULTIPLES. Now, for this case, that’s not really too hard, but hopefully you can imagine with more complicated code, this becomes a hassle. Indeed, suppose you are write a program, and want to improve how the program works. Having that piece of the algorithm in its own procedure makes it much easier to change, if you need to.

So, let’s create a procedure that prints out the first MAX_NUM_MULTIPLES of NUMBER. To do this, I will call it multipleSum(), and use the def command to create this procedure. This is done in the program below. The code in the procedure multipleSum() is very similar to what was given above. The only difference comes from since multipleSum() takes two arguments. An argument is something I pass to the function or procedure for its use. This can be a variable, a list, or some other possibilities we will not worry about. The arguments are defined outside the function or procedure, which can perform operations on these quantities. Getting back to our procedure, the two arguments of multipleSum() are the values NUMBER and MAX_NUM_MULTIPLES. Every time we call this procedure, we can specify the values of these variables, without having to change any code! At the end, it prints out the result total.

Back to program list

To find the first five multiples of seven, you now need to call the procedure. You do this by writing the command

multipleSum(7, 5)

Notice the order – this defines NUMBER as 7, and MAX_NUM_MULTIPLES as 5, since the numbers are matched with the variable names in the procedure code. Running the program, the computer should print out 105 again.

Problem

What would you expect to be printed out if you write multipleSum(5, 7) instead? Calculate the answer first, then run the command with the arguments flipped to check your answer.

Problem

Use multipleSum() to find the first eight multiples of 15. Type in the appropriate code in the Trinket app above.

Answer: You can get the answer using the function multipleSum() by running

multipleSum(15, 8)

You should get 540.

So a procedure executes some code, which can be called on later (and mulitple times!) by the main program. A function is slightly different, in that it returns information to the main program. Specifically, suppose instead of printing the first MAX_NUM_MULTIPLES of NUMBER, we want to use this information to define another variable, say result. We couldn’t do that with the procedure above. This is a case where we want to write a function. The crucial change with a function is that there is a command return that “passes back” the computed value total, and can be used later.

As an example, we could define a function add() that adds together two numbers num1 and num2, as follows.

def add(num1, num2):
    return num1 + num2

The return statement means that the result of this function is similar to how a variable is defined. If you write add(firstNum, secondNum), then the computer will associate a value firstNum + secondNum to it. Then this could be used in another place in the program:

thirdNum = add(firstNum, secondNum)

We couldn’t do this with our procedures from before, since they just printed out the result. Also, notice the variable names when the function (or procedure) is used do not have to be the same as those in the code for the function itself, but they do have to be in the same, matching order!

Problem

Change the procedure multipleSum() in the program above so that it returns the value total.

Answer: Your code should look like the following, with the only change on the last line:

def multipleSum(NUMBER, MAX_NUM_MULTIPLES):
    
    total = 0
    numMultiples = 0
    
    while numMultiples < MAX_NUM_MULTIPLES:
        numMultiples += 1
        total += numMultiples * NUMBER
        
    return total

Problem

Write a Python function multipleProduct() that find the product of all integers from 1 to a given number. The argument of the function NUMBER is the final integer you will multiply in the product. If NUMBER is less than or equal to zero, then have the program print out “Must use positive numbers”, and return the value zero. Note: In mathematics, this is also known as the factorial, with the notation that the factorial of the number \(n\) is \(n!\).

Answer: Here is a possible program to create multipleProduct().

def multipleProduct(NUMBER):

    # Check if NUMBER is positive
    
    if NUMBER <= 0:
        print('Must use positive numbers')
        return 0
        
    product = 1              # Starting value of product
    nextNum = 1              # Next number to multiply in product
    
    while nextNum < NUMBER:
        nextNum += 1         # Increase nextNum to nextInteger
        product *= nextNum   # Multiply next integer and product
        
    # Return product
    
    return product

Notice that the order of the statements inside the while loop is important; switching this order will lead to the last integer not being included in the product.

1.7. Example: Calculating square roots

Can’t the computer find this?

You may wonder why we just can’t ask the computer to do this calculation. Well, first, it’s good to know what your computer is actually doing! Plus this is good practice for applying the methods of this lesson. Finally, there is a way to find the square root, but it is not automatically included in Python. Instead, it is part of the math module of Python. I will introduce modules in Lesson 02.

Now I will go through an example that brings together a lot of what is covered in the lesson. By the end, we will have a function that calculates the square root of a given positive number. The method used here is known as “Heron’s method”, after the 1st century AD Greek mathematician Heron of Alexandria. It is also known as “the Babylonian method”, since it is believed (but not proven) that the ancient Babylonians were also aware of this method. Although there are now more sophisticated means of finding roots, this will give you some idea of how your calculator gets the number!

Here is the basic idea. Suppose we want to know the square root of the number \(c\). Thus, we are trying to solve the equation \(x^2 - c = 0\). We can make a guess \(g\) for what the square root is; for example, we can guess that the square root of two is \(g = 1\). Obviously, this is wrong, so there is some error \(e\) that our guess is off by. This means that we have \((g + e)^2 = c\). Let’s solve this equation for \(e\); if we expand it out, we have

\[ g^2 + 2g e + e^2 = c \Rightarrow e = \frac{c - g^2}{2g + e} \]

Now, let’s use the fact that (hopefully) our error \(e\) is smaller than \(2g\), so we approximate the above equation by

\[ e \simeq \frac{c - g^2}{2g} \]

Note that the symbol “\(\simeq\)” means “approximately equal to”. This means our new guess \(g'\) for the square root of \(c\) is

\[ g' = g + e = g + \frac{c - g^2}{2g} = \frac{g^2 + c}{2g} = \frac{g + c/g}{2} \]

We can then use this new guess \(g'\), and find its error away from the real value. Repeating this process over and over gets our guess closer to the actual value. Notice that our new guess \(g'\) is simply the average of our original guess \(g\), and the number \(c\) we are trying to find the square root of divided by \(g\). One of these numbers will be greater than the real root, while the other will be smaller. This is why the average of the two will get us closer to the actual root.

The code below shows how to find \(\sqrt{2}\). Notice that it only takes a few steps to get a really good value!

Back to program list

Obviously, this is great for printing out \(\sqrt{2}\), but suppose we want to use it to define a variable? Or find the square root of another number? Then we need to write a function for this. This is done in the program given further below, where a function squareRoot() is defined, with two arguments NUMBER and NUM_STEPS. These are the two constant values from the previous program, so it is natural they are what we input when using the function.

A few notes about this function. First, I removed the print statements, but you can always put them back if you want to see how the method is progressing. I also have included what is known as a docstring (short for documentation string) at the beginning of the function, in between the triple single quotes (you can also use double quotes, if you wish). This provides a place for the programmer to document their code for other users. These are read in Python like a comment, but without having to put a # at the beginning of every line. This is good practice, to explain to anyone reading the code what it is trying to do, and how.

Finally, notice that I have assigned a value to NUM_STEPS. What does this mean? This is a default value for the number of steps of the function. Run this code now, then we can come back to this point.

Back to program list

By the way, notice that we cannot use the += operator for guess inside the for loop, since we are not simply adding a number to guess, but we are doing something more complicated.

Problem

Add the appropriate command to the program above to print out the results of the function squareRoot(), when finding the square root of 2 using seven steps.

Answer: Using squareRoot(2, 7) will run the function, to find the square root of 2 with seven steps. However, it will not print out the value it found. Thus, you must use the command

print(squareRoot(2, 7))

This should print out the value 1.41421356237.

For the above, I put the two arguments NUMBER and NUM_STEPS as 2 and 7, respectively. But what if I don’t care how many steps the method takes? This is why I put a default value. If I only put one argument, then Python will assign its value to NUMBER, and automatically take NUM_STEPS to be 5. Add the line

print(squareRoot(2))

and run the program. This uses five steps to find \(\sqrt{2}\), since we did not specify NUM_STEPS.

Problem

Find the square root of your favorite number. See many steps does it take to match what your calculator says if you use it instead.

You may have caught it already, but there are several issues with this method, as written in our function. The first question is how do we deal with negative numbers? It’s probably good policy to just not deal with those! So, go back to the original function, and add the following if statement just before the definition of guess:

if NUMBER <= 0:
    print('We only find the square roots of positive numbers.')
    return 0

This will print a warning, then return the value 0.

The second issue is that our original guess is really bad! We can do much better than that. One way to improve our guess is to start a variable guess with value 1, and see if squaring this number gives a value greater than NUMBER. If not, we can increase guess by one, and see if its square is greater than NUMBER. Eventually, it will be, so we use this value as the start for Heron’s method. Notice we don’t care if we go over the value of NUMBER, since the method uses NUMBER / guess (which will be lower than the number we want the root of) in the average to find the next guess. To implement this, after the definition of guess, but before the for loop, type in the code

while guess ** 2 < NUMBER:
    guess += 1

Now run the improved procedure with different values of NUMBER, and see how it does. You should get much better results than before.

Problem

You can modify the method given above to find the cube root of a number. Suppose we want to find the cube root of \(c\), i.e. find the value \(x\) such that \(x^3 - c = 0\). If we make a guess \(x = g\) with an integer \(g\), then in general this will be off by some error \(e\), such that \((g + e)^3 = c\). Multiplying this out, we have

\[ g^3 + 3 g^2 e + 3 g e^2 + e^3 = c \]

Like before, we assume that \(e\) is small, and approximate this equation by dropping both the \(e^2\) and \(e^3\) terms. Then, solving for our next guess \(g'\), we have

\[ g' = g + e = \frac{1}{3} \biggl(\frac{c}{g^2} + 2g \biggr) \]

Using this method, write a Python function cubeRoot() that calculates the cube root of a given number. The function should have two arguments: NUMBER, the number to take the cube root of, and NUM_STEPS, the number of steps to use in the algorithm. What would be a way of getting a good first guess for the cube root?

Answer: Here is one possible program. The initial guess uses the same method as above, by finding the integer whose cube is the lowest one above the given number.

def cubeRoot(NUMBER, NUM_STEPS = 5):
    '''
    Find the cube root of a number
    '''
    
    guess = 1        # Starting guess for the root

    while guess ** 3 < NUMBER:
        guess += 1

    for iii in range(NUM_STEPS):
        guess = (NUMBER / guess ** 2 + 2 * guess) / 3
    
    return guess     # Final value of method

Notice we don’t have to worry about whether the original number is positive or negative, since you can take the cube root of a negative number!

1.8. Summary

This lesson covers a lot of the Python ideas and commands you will use in other lessons. In particular, it covers variables, mathematical operations, while and if statements, lists, logical tests, and functions and procedures. It may seem like a lot, but with practice, you will get used to it all. You should review this lesson every once in a while, to make sure you haven’t forgotten anything, or if you need a reminder of how a particular command works. Note that this is a rather simplified version of Python – there are many other commands that we will not use in these lessons. However, it does give you a basic familiarity with the language. If you are interested in learning more, there are many resources on-line, since Python is a very popular language. If you sign up for a free Trinket account, you can find some helpful introductions on the Home page of your account, under “Featured Courses”. Two other sites I find nice are w3schools.com and Easy Python Docs; just realize they feature the entire language!

After this lesson, you should be able to:

• Create numerical variables, and print the values of these variables

• Use mathematical operators to change the value of a variable

• Use an if statement to make a logical test

• Create a while or for loop

• Create a list

• Create a procedure or function with arguments

NAPS Intermediate Physics 2. Vectors and vPython